Teori Graf merupakan suatu diagram yang memuat informasi tertentu jika diinterpretasikan secara tepat. Dalam kehidupan sehari-hari graf digunakan untuk mengambarkan berbagai macam struktur yang ada. Tujuannya adalah sebagai visualisasi objek-objek agar lebih mudah dimengerti.
Beberapa contoh graf yang sering dijumpai, antara lain struktur organisasi, bagan alir, pengambilan mata kuliah, peta, rangkaian listrik, dan lain-lain (Hendardi, 2012).
Banyak sekali struktur yang bisa dipresentasikan dengan graf, dan banyak masalah yang bisa diselesaikan dengan graf. Sering kali graf digunakan untuk mempresentasikan suatu jaringan. Misalkan jaringan jalan raya dengan kota sebagai simpul ( vertex ) dan jalan yang menghubungkan setiap kota sebagai sisi ( edge ) dan bobotnya ( weight ) adalah panjang dari jalan tersebut.
Secara matematis graf mendefinisikan sebagai pasangan himpunan (V, E), ditulis dengan notasi G = (V, E), yang dalam hal ini V adalah himpunan tidak kosong dari simpul-simpul ( vertex atau node ) dan E adalah himpunan sisi ( edge ) yang menghubungkan sepasang simpul (Munir, R. 2009)
Simpul ( vertex ) pada graf dapat dinyatakan dengan huruf, bilangan atau gabungan keduanya. Sedangkan sisi-sisi yang menghubungkan simpul u dengan simpul v dinyatakan dengan pasangan (u, v) atau dinyatakan dengan lambang ππ1, ππ2, ππ3 dan seterusnya.
Teori Dasar Graf
Graf G didefinisikan sebagai pasangan himpunan (V,E), ditulis dengan notasi G=(V,E), yang dalam hal ini V adalah himpunan tidak kosong dari simpul-simpul dan E adalah himpunan sisi yang menghubungkan sepasang simpul (Munir, R. 2005).
Garis yang hanya berhubungan dengan satu titik ujung disebut loop . Dua garis berbeda yang menghubungkan titik yang sama disebut garis paralel. Dua titik dikatakan berhubungan ( adjacent ) jika garis menghubungkan keduanya. Titik yang tidak memiliki garis yang berhubungan dengannya disebut titik terasing ( isolating point ). Graf yang tidak memiliki titik (sehingga tidak mewakili garis) disebut garis kosong.
Jika semua garisnya berarah, maka grafnya disebut graf berarah ( directed graph ), atau sering disingkat di graph . Jika semua garisnya tidak berarah, maka grafnya disebut graf tak berarah ( undirected graph ). Sehinga dapat ditinjau dari arahnya, graf dapat dibagi menjadi dua yaitu graf berarah dan graf tidak berarah.
Graf Berarah (Directed Graf = Digraph)
Pada graf berarah, arah sisi/urutan ikut diperhatikan. Dalam suatu graf, lintasan ( path ) adalah urutan simpul, atau sisi yang dibentuk untuk bergerak dari satu simpul ke simpul yang lain. Dalam graf berarah, titik akhir dari sebuah busur akan menjadi titik awal dari busur berikutnya. Sirkuit adalah lintasan yang memiliki simpul awal dan akhir yang sama. Panjang lintasan adalah banyaknya sisi yang dilalui lintasan tersebut.
Suatu Graf berarah G terdiri dari himpunan titik-titik V(G) {π£π£1, π£π£2, β¦}, himpunan garis-garis E(G) {ππ1, ππ2, β¦ }, dan suatu fungsi yang mengawankan setiap garis dalam E(G) ke suatu pasangan berurutan titik (π£π£ππ , π£π£ππ ). Jika ππππ = (π£π£ππ , π£π£ππ ) adalah suatu garis dalam G, maka π£π£ππ disebut titik awal ππππ dan π£π£ππ disebut titik akhir ππππ . Arah garis adalah dari π£π£ππ ke π£π£ππ .
Jumlah garis yang keluar dari titik π£π£ππ disebut derajat keluar ( out degree ) titik π£π£ππ yang disimbolkan dengan ππ+(π£π£ππ ), sedangkan jumlah garis yang menuju ke titik π£π£ππ disebut derajat masuk ( in degree ) titik π£π£ππ , yang disimbolkan dengan ππβ(π£π£ππ ).
Titik terasing adalah titik dalam G dimana derajat keluar dan derajat masuknya adalah 0. Titik pendant (tergantung) adalah titik dalam G dimana derajat masuk dan derajat keluarnya adalah 1. Dua garis berarah dikatakan paralel jika keduanya memiliki titik awal dan titik akhir yang sama.
Contoh
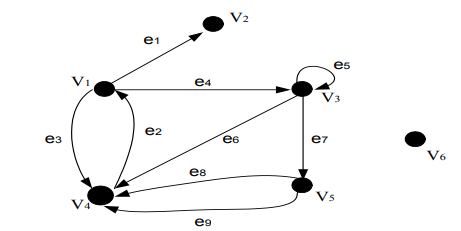
Gambar Graf Berarah
Tentukan:
- Himpunan titik-titik, himpunan garis-garis, dan fungsi perkawanan.
- Derajat masuk dan derajat keluar tiap titik.
- Titik terasing dan titik pendant.
- Garis paralel.
Penyelesaian:
a. V(G) = { π£π£1, π£π£2, π£π£3, π£π£4, π£π£5, π£π£6 }
E(G) = { ππ1, ππ2, ππ3, ππ4, ππ5, ππ6, ππ7, ππ8, ππ9 }
Fungsi mengawankan garis-garis dengan pasangan titik-titik berikut
ππ1 dengan (π£π£1, π£π£2)
ππ2 dengan (π£π£4, π£π£1)
ππ3 dengan (π£π£1, π£π£4)
ππ4 dengan (π£π£1, π£π£3)
ππ5 dengan (π£π£3, π£π£3)
ππ6 dengan (π£π£3, π£π£4)
ππ7 dengan (π£π£3, π£π£5)
ππ8 dengan (π£π£5, π£π£4)
ππ9 dengan (π£π£5, π£π£4)
b.
| ππ+ (π£π£1) = 3 |
ππβ (π£π£1) = 1 |
| ππ+ (π£π£2) = 0 |
ππβ (π£π£2) = 1 |
| ππ+ (π£π£3) = 3 |
ππβ (π£π£3) = 2 |
| ππ+ (π£π£4) = 1 |
ππβ (π£π£4) = 4 |
| ππ+ (π£π£5) = 2 |
ππβ (π£π£5) = 1 |
| ππ+ (π£π£6) = 0 |
ππβ (π£π£6) = 0 |
Dapat dilihat bahwa dalam setiap graf berarah, βππ ππ+ (π£π£ππ) = βππ ππβ (π£π£ππ)
c. Titik terasing adalah π£π£6.
Titik pendant π£π£2.
d. Garis paralel adalah ππ8 dan ππ9, dapat dilihat bahwa ππ2 dan ππ3 bukanlah garis paralel karena arahnya berbeda.
Path Berarah dan Sirkuit Berarah
Pengertian walk, path, dan sirkuit dalam graf berarah sama dengan walk, path dan sirkuit dalam graf tak berarah. Hanya saja dalam graf berarah, perjalanan yang dilakukan harus mengikuti arah garis. Untuk membedakan dengan graf tak berarah, maka walk, path berarah, dan sirkuit dalam graf berarah disebut walk berarah, path berarah, dan sirkuit berarah. Suatu graf berarah yang tidak memuat sirkuit berarah disebut Asiklik (Siang, 2009).
Contoh
Ada 4 macam golongan darah, masing-masing A, B, AB, dan O. Darah golongan O dapat diberikan kepada semua golongan. Darah golongan A dan B dapat diberikan ke golongannya sendiri atau ke golongan O. Darah golongan AB hanya dapat diberikan pada pasien dengan golongan darah AB . Gambarkan graf berarah untuk menyatakan keadaan tersebut. Anggaplah garis dari π£π£ππ ke π£π£ππ menyatakan bahwa darah dari π£π£ππ dapat diberikan pada π£π£ππ .
Apakah graf Asiklik?
Penyelesaian:
Graf berarah menyatakan keadaan transfusi darah yang mungkin dilakukan. Dapat dilihat bahwa dalam graf berarah tersebut tidak ada sirkuit berarah sehingga grafnya Asiklik.
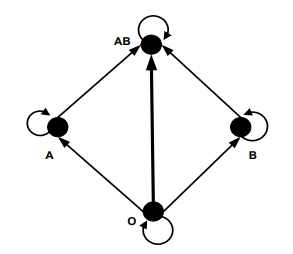
Gambar Path berarah**
Graf Berarah Terhubung
Suatu graf tak berarah disebut terhubung jika ada walk yang menghubungkan setiap dua titiknya. Pengertian itu berlaku juga bagi graf berarah. Berdasarkan arah garisnya, dalam graf berarah dikenal dua jenis keterhubungan, yaitu terhubung kuat dan terhubung lemah.
Misalkan G adalah suatu graf berarah dan v, w adalah sembarang 2 titik dalam G. G disebut terhubung kuat jika ada path berarah dari v ke w. G disebut terhubung lemah, jika G tidak terhubung kuat, tetapi graf tak berarah yang bersesuaian dengan G terhubung.
Contoh
Manakah di antara graf-graf pada Gambar dibawah ini .yang terhubung kuat dan yang terhubung lemah?
Gambar Graf berarah terhubung
Penyelesaian:
Dalam πΊπΊ1, setiap dua titik dapat dihubungkan dengan path berarah sehingga graf berarah πΊπΊ1 adalah graf terhubung kuat. Sebaliknya dalam πΊπΊ2, tidak ada path berarah yang menghubungkan π£π£4 ke π£π£3. Akan tetapi, jika semua arah garis dihilangkan (sehingga πΊπΊ2 menjadi graf tidak berarah), maka πΊπΊ2 merupakan graf yang terhubung. Jadi, πΊπΊ2 merupakan graf terhubung lemah.
Isomorfisma dalam Graf Berarah
Pengertian isomorfisma dalam graf berarah sama dengan isomorfisma pada graf tak berarah. Hanya saja pada isomorfisma graf berarah, korespondensi dibuat dengan memperhatikan arah garis.
Contoh
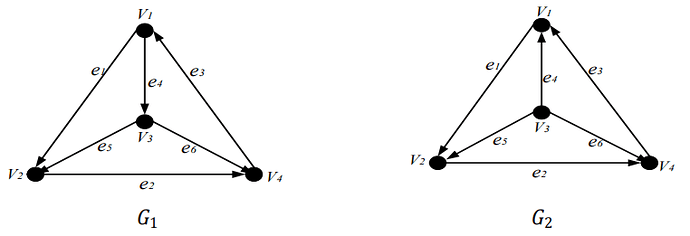
Tunjukkan bahwa graf πΊπΊ1 pada Gambar di bawah ini isomorfis dengan πΊπΊ2, sedangkan πΊπΊ3 tidak isomorfis dengan πΊπΊ1
Gambar Isomofisma dalam Graf Berarah
Penyelesaian:
Untuk membuktikan bahwa πΊπΊ1 isomorfis dengan πΊπΊ2, maka harus dibuat fungsi g : V(πΊπΊ1) β V(πΊπΊ2) dan h : E(πΊπΊ1) β E(πΊπΊ2) yang mempertahankan titik-titik ujung serta arah garis.
Dalam πΊπΊ1, ada 4 garis yang keluar dari ππ3. Titik yang memiliki sifat seperti itu dalam πΊπΊ2 adalah titik π£π£1, sehingga dibuat fungsi g sedemikian hingga g(π£π£3) = π£π£1, g(π£π£1) = π£π£2, g(π£π£2) = π£π£3, g(π£π£5) = π£π£4, dan g(π£π£4) = π£π£5
fungsi h adalah sebagai berikut:
h ((π£π£1, π£π£2)) = (π£π£2, π£π£3) ; h ((π£π£2, π£π£5)) = (π£π£3, π£π£4) h ((π£π£5, π£π£4)) = (π£π£4, π£π£5) ; h ((π£π£4, π£π£1)) = (π£π£5, π£π£2) h ((π£π£3, π£π£1)) = (π£π£1, π£π£2) ; h ((π£π£3, π£π£2)) = (π£π£1, π£π£3) h ((π£π£3, π£π£5)) = (π£π£1, π£π£4) ; h ((π£π£3, π£π£4)) = (π£π£1, π£π£5)
pada fungsi g dan h dapat dilihat bahwa πΊπΊ1 isomorfis dengan πΊπΊ2. Selanjutnya, akan dibuktikan bahwa πΊπΊ3 tidak isomorfis dengan πΊπΊ1. Dalam πΊπΊ3, ada garis (π£π£1, π£π£4) dan (π£π£4, π£π£1). Jika πΊπΊ1 isomorfis dengan πΊπΊ3, maka harus ada fungsi h πΊπΊ3 β πΊπΊ1 demikian, sehingga h(π£π£1, π£π£4) dan h(π£π£4, π£π£1) merupakan garis-garis dalam πΊπΊ1 (dengan kata lain, ada titik π£π£ππ dan π£π£ππ dalam πΊπΊ1 demikian, sehingga ada garis dari π£π£ππ ke π£π£ππ dan dari π£π£ππ ke π£π£ππ ). Dalam πΊπΊ1 tidak ada garis seperti itu sehingga πΊπΊ3 tidak isomorfis dengan πΊπΊ1.
Graf Tak Berarah (Undirected Graph)
Suatu graf G terdiri dari dua himpunan yang berhingga, yaitu himpunan simpul-simpul tak kosong (V(G)) dan himpunan jalur-jalur (E(G)). Jika semua jalurnya tidak berarah, maka grafnya disebut graf tak berarah (Siang, J.J. 2009).
Graf Bipartite (Bipartite Graph)
Suatu graf G disebut Graf Bipartite apabila V(G) merupakan gabungan dari dua himpunan tak kosong π£π£1 dan π£π£2 dan setiap garis dalam G menghubungkan suatu titik dalam π£π£1 dengan titik dalam π£π£3. Apabila dalam Graf Bipartite setiap titik dalam π£π£1 berhubungan dengan setiap titik dalam π£π£2, maka grafnya disebut Graf Bipartite lengkap. Jika π£π£1 terdiri dari m titik dan π£π£2 terdiri dari n titik, maka Graf Bipartite lengkapnya sering diberi simbol πΎπΎππ ,ππ .
Contoh
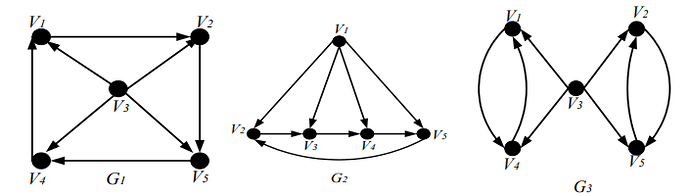
Tentukan mana di antara graf-graf pada Gambar dibawah ini yang merupakan Graf Bipartite dan Bipartite Lengkap.
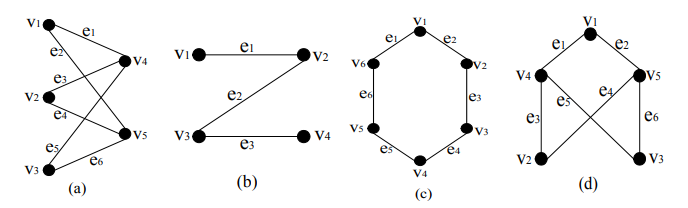
Gambar Graf Bipartite
Penyelesaian:
a. Jelas bahwa titik-titik grafnya terbagi menjadi dua bagian, yaitu π£π£1 = {π£π£1, π£π£2, π£π£3} dan π£π£2 = {π£π£4, π£π£5}. Setiap titik dalam π£π£1 dihubungkan dengan setiap titik dalam π£π£2 sehingga grafnya merupakan πΎπΎ3,2.
b. Hanya merupakan Graf Bipartite saja karena titik-titik dalam graf terbagi menjadi dua bagian, yaitu π£π£1 = {π£π£1, π£π£3} dan π£π£2 = {π£π£2, π£π£4}. Akan tetapi tidak semua titik dalam π£π£1 dihubungkan dengan semua titik dalam π£π£2 (π£π£1 tidak dihubungkan dengan π£π£4).
c. Dengan pengaturan letak titik-titiknya, maka graf gambar Β© dapat digambarkan sebagai graf.
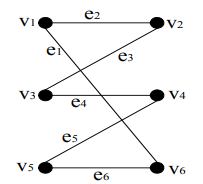
Tampak bahwa titik-titiknya terbagi menjadi dua bagian, yaitu π£π£1 = {π£π£1, π£π£3, π£π£5} dan π£π£2 = {π£π£2, π£π£4, π£π£6}. Setiap menghubungkan sebuah titik dalam π£π£1 dengan sebuah titik dalam π£π£2 sehingga grafnya merupakan Graf Bipartite.
d. Bila dilihat bahwa meskipun tampil berbeda, sebenarnya graf pada Gambar bagian (d) sama dengan graf pada Gambar bagian (a) sehingga graf pada Gambar bagian (d) adalah πΎπΎ3,2.
Posisi titik-titik dalam penggambaran graf kadang-kadang mempengaruhi pandangan, seperti halnya pada Gambar bagian Β© dan (d). Dalam kedua graf tersebut, semua titik tampaknya terhubung dan tidak dapat dipisahkan walaupun kenyataannya tidaklah demikian. Oleh karena itu harus jeli dalam menentukan apakah suatu graf merupakan Graf Bipartite.
SubGraf
Konsep subgraf sama dengan konsep himpunan bagian. Dalam teori himpunan, himpunan A dikatakan merupakan himpunan bagian B bila hanya setiap anggota A merupakan B. Oleh karena graf merupakan himpunan yang terdiri dari titik dan garis, maka H dikatakan subgraf G, jika semua titik dan garis H juga merupakan titik dan garis dalam G. Secara formal, subgraf dapat didefinisikan sebagai berikut.
Misalkan G adalah suatu graf. Graf H dikatakn subgraf G bila dan hanya bila
- V(H) β V(G)
- E(H) β E(G)
- Setiap garis dalam H memiliki titik ujung yang sama dengan garis tersebut dalam G.
Dari definisi tersebut ada beberapa hal yang dapat diturunkan
-
Sebuah titik dalam G merupakan subgraf G.
-
Sebuah garis dalam G bersama-sama dengan titik-titik ujungnya merupakan subgraf G.
-
Dalam subgraf berlaku sifat transitif, jika H adalah subgraf G dan G adalah subgraf K, maka K adalah subgraf K.
Contoh
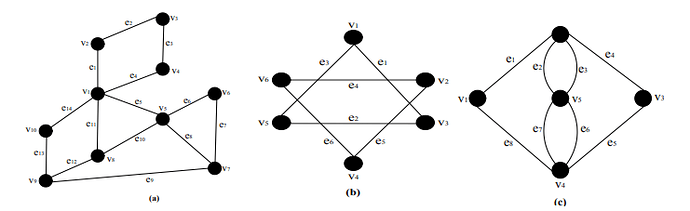
Gambarlah semua Subgraf yang mungkin dibentuk dari graf G pada Gambar dibawah ini.
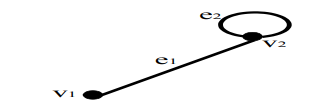
Gambar Sub Graf
Penyelesaian:
G terdiri dari dua titik dan dua garis. Subgraf G yang mungkin dibentuk terdiri dari satu atau dua titik dan 0, satu atau dua garis. Semua Subgraf G yang mungkin dibuat dapat digambarkan sebagai berikut:
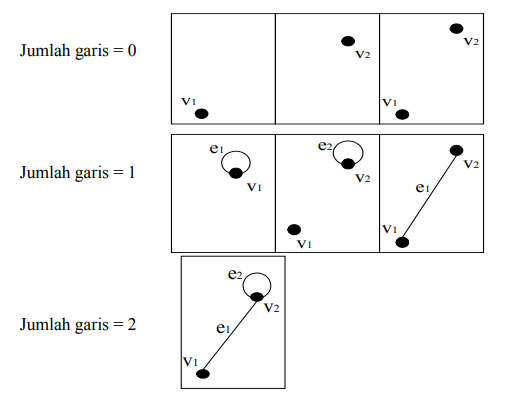
Gambar Sub-Graf dari Gambar di atas
Derajat (Degree)
Misalkan v adalah titik dalam suatu graf G. derajat titik v (simbol d(v)) adalah jumlah garis yang berhubungan dengan titik v dan garis suatu loop dihitung dua kali. Derajat total G adalah jumlah derajat semua titik dalam G.
Contoh
Tentukan derajat tiap-tiap titik dalam graf pada Gambar di bawah ini. Berapa derajat totalnya
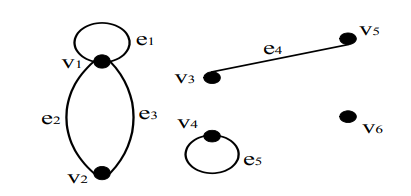
Gambar Derajat (Degree)
Penyelesaian:
d (π£π£1) = 4 garis yang berhubungan dengan π£π£1 adalah ππ2, ππ3 dan loop ππ1 yang dihitung dua kali.
d (π£π£2) = 2 garis yang berhubungan dengan π£π£2 adalah ππ2 dan ππ3.
d (π£π£3) dan d (π£π£5) = 1 karena garis yang berhubungan dengan π£π£3 dan π£π£5 adalah ππ4.
d (π£π£4) = 2 garis yang berhubungan dengan π£π£4 adalah loop ππ5 yang dihitung dua kali. d (π£π£6) = 0 karena tidak ada garis yang berhubungan dengan π£π£6.
Derajat total = β6 ππ (π£π£ππ) = 4 + 2 + 1 + 2 + 1 + 0 = 10.
Path dan Sirkuit
Misalkan G adalah suatu graf. Misalkan pula v dan w adalah dua titik dalam G. Suatu Walk dari v dan w adalah barisan titik-titik berhubungan dan garis secara berselang-selang, diawali dari titik v dan diakhiri pada titik w.
Walk dengan panjang n dan v ke w dituliskan sebagai berikut π£π£0 ππ1 π£π£1 ππ2 π£π£2β¦ π£π£ππβ1 ππππ π£π£ππ dengan π£π£0 = v, π£π£ππ = w, π£π£ππ β1, dan π£π£ππ adalah titik-titik ujung garis ππππ . Path dengan panjang n dari v ke w adalah walk dari v ke w yang semua garisnya berbeda. Path dari v ke w dituliskan sebagai v = π£π£0 ππ1 π£π£1 ππ2 π£π£2β¦ π£π£ππβ1 ππππ π£π£ππ = w dengan ππππ β w untuk i β j.
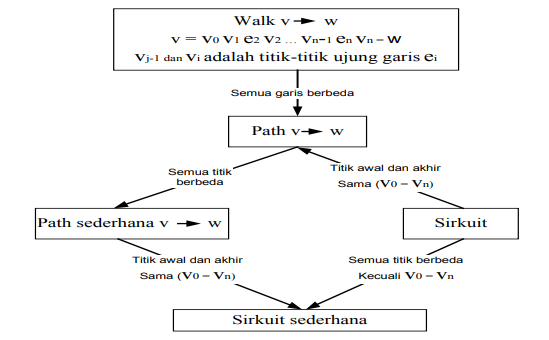
Gambar Bagan Alur Path dan Sirkuit
Path sederhana dengan panjang n dan v ke w adalah path dari v ke w berbentuk v = π£π£0 ππ1 π£π£1 ππ2 π£π£2β¦ π£π£ππβ1 ππππ π£π£ππ = w dengan ππππ β w untuk i β j dan π£π£ππ β π£π£ππ untuk k β m. Sirkuit dengan panjang n adalah path yang dimulai dan diakhiri pada titik yang sama. Sirkuit adalah path yang berbentuk v = π£π£0 ππ1 π£π£1 ππ2 π£π£2β¦ π£π£ππβ1 ππππ π£π£ππ = w dengan π£π£0 = π£π£ππ . Sirkuit sederhana dengan panjang n adalah Sirkuit yang semua titiknya berbeda. Sirkuit sederhana berbentuk v = π£π£0 ππ1 π£π£1 ππ2 π£π£2β¦ π£π£ππβ1 ππππ π£π£ππ = w dengan ππππ β ππππ untuk i β j dan π£π£ππ β π£π£ππ untuk k β m, kecuali π£π£0 = π£π£ππ .
Sirkuit Euler
Sirkuit Euler adalah Sirkuit yang melalui tiap sisi dalam graf tepat satu kali (Siang, J.J. 2009) Untuk mengenang ahli matematika Leonhard Euler yang berhasil memperkenalkan graf untuk memecahkan masalah tujuh jembatan Koningsberg pada tahun 1736.
Kota Koningberg dibangun pada pertemuan dua cabang sungai Pregel. Kota tersebut terdiri dari sebuah pulau di tengah-tengah dan tujuh jembatan yang mengelilinginya.
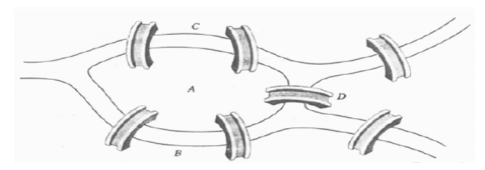
Gambar Jembatan Konigsberg
Graf Terhubung dan Tidak Terhubung
Misalkan G adalah suatu Graf. Dua titik v dan w dalam G dikatakan terhubung hanya ada walk dari v ke w. Graf G dikatakan terhubung bila hanya setiap dua titik dalam G terhubung. Graf G dikatakan tidak terhubung bila ada dua titik dalam G yang tidak terhubung.
Contoh
Tentukan mana di antara graf pada Gambar dibawah ini yang merupakan Sirkuit Euler. carilah rute perjalanan kelilingnya
Gambar Graf terhubung dan Graf tak terhubung
Penyelesaian:
a. d(π£π£2) = d(π£π£3) = d(π£π£4) = d(π£π£6) = d(π£π£10) = 2
d(π£π£5) = 4
d(π£π£7) = d(π£π£8) = d(π£π£9) = 3
d(π£π£1) = 5
karena ada titik yang berderajat ganjil, maka (a) bukanlah Sirkuit Euler.
b. Meskipun semua titiknya berderajat dua (genap), tetapi grafnya tidak terhubung. Jadi, (b) bukanlah Sirkuit Euler.
c. d(π£π£1) = d(π£π£3) = 2
d(π£π£2) = d(π£π£4) = d(π£π£5) = 4
karna graf ( c) terhubung dan semua titiknya berderajat genap, maka ( c) merupakan Sirkuit Euler.
Sirkuit Hamilton
Suatu graf terhubung G disebut Sirkuit Hamilton bila ada sirkuit yang mengunjungi setiap titiknya tepat satu kali kecuali titik awal yang sama dengan titik akhirnya.
Perhatikan perbedaaan Sirkuit Euler dan Sirkuit Hamilton. Dalam Sirkuit Euler, semua garis harus dilalui tepat satu kali, sedangkan semua titiknya boleh dikunjungi lebih dari satu kali. Sebaliknya, dalam Sirkuit Hamilton semua titik harus dikunjungi tepat satu kali dan tidak harus melalui semua garis. Dalam Sirkuit Euler, yang dipentingkan adalah garisnya. Sebaliknya dalam Sirkuit Hamilton, yang dipentingkan adalah kunjungan pada titiknya(Munir, R. 2009).
