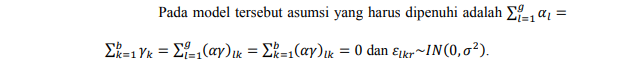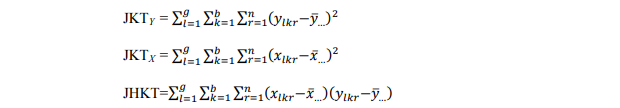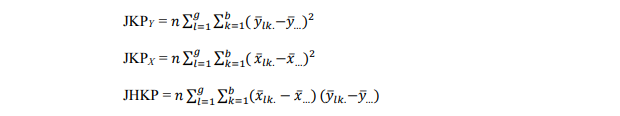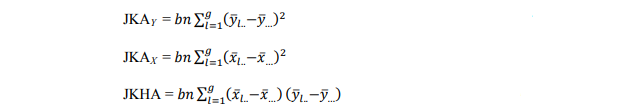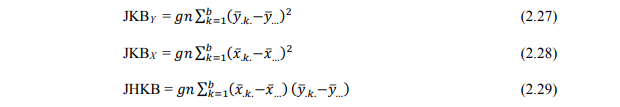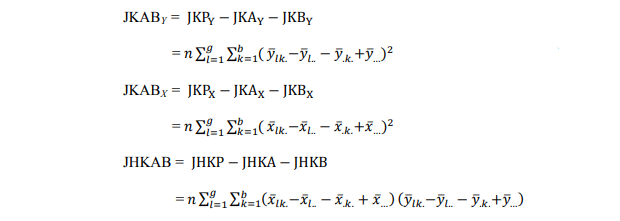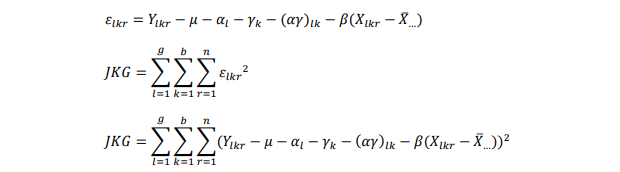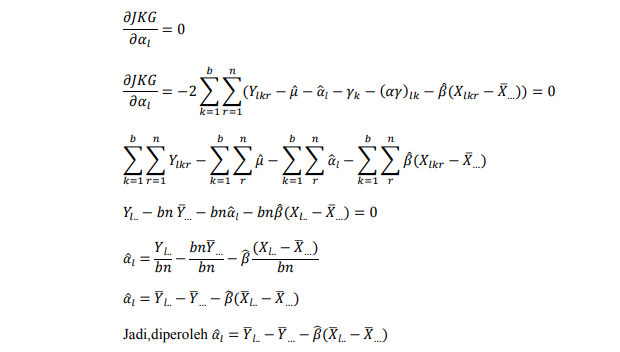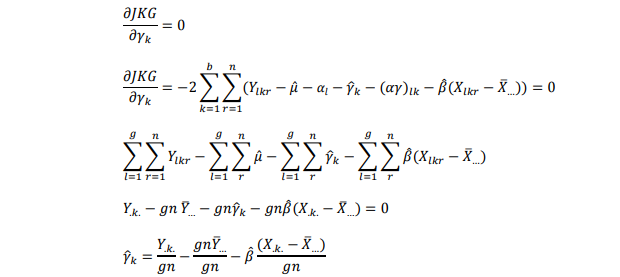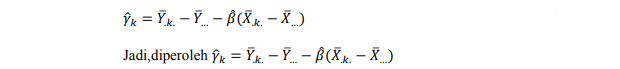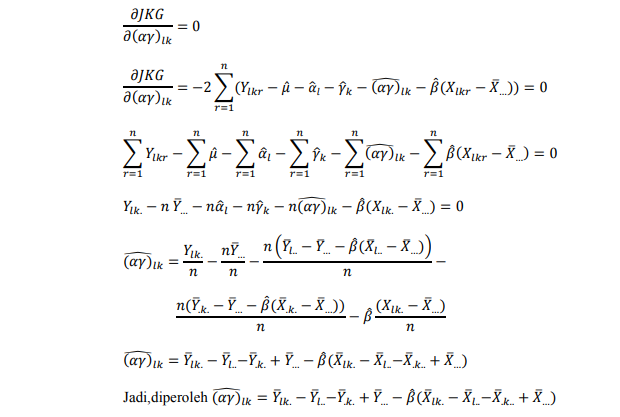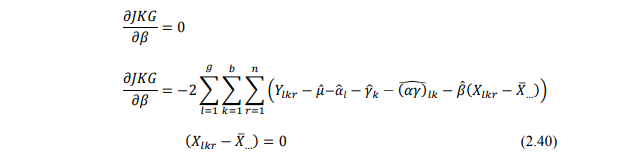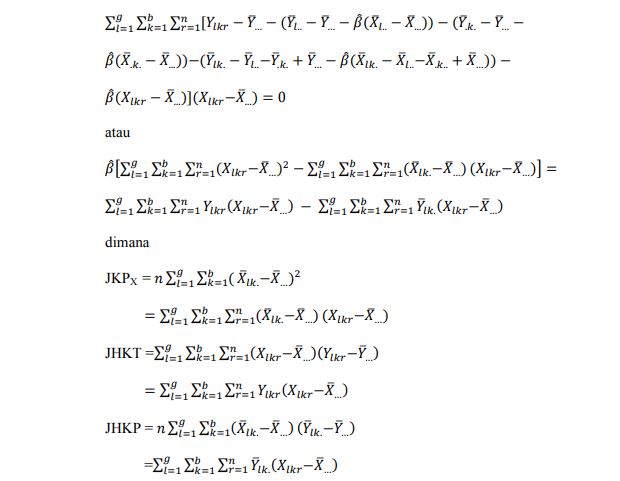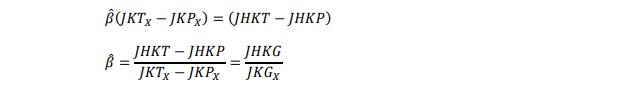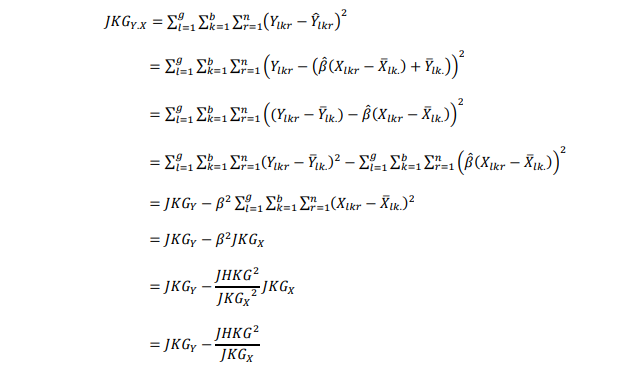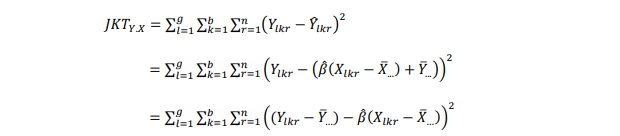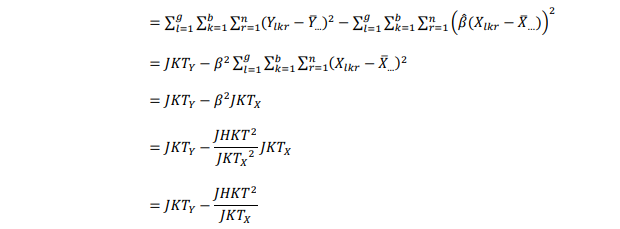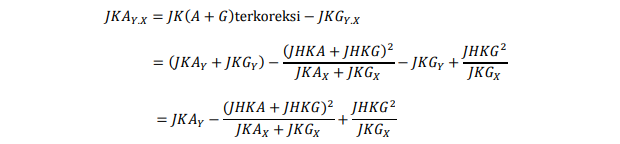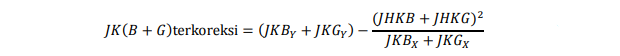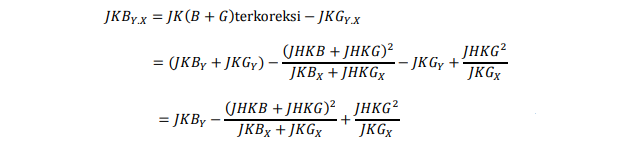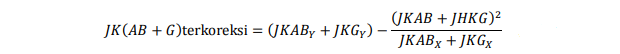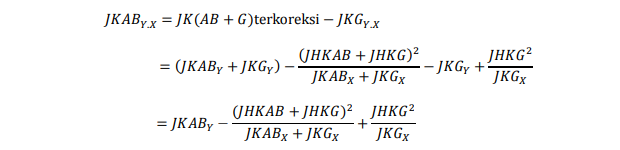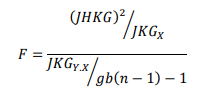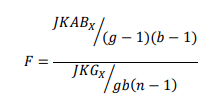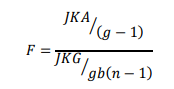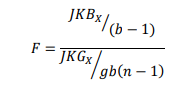Analisis Kovarians (ANCOVA) merupakan model linier dengan satu variabel dependen kontinu dan satu atau lebih variabel independen. ANCOVA merupakan penggabungan antara ANOVA dan regresi linier yang lazimnya menggunakan variabel kontinu (kuantitatif). ANCOVA dilakukan dengan menambahkan variabel penguat (kovariat) ke dalam model sehingga memperkuat ketepatan/presisi analisis dan meningkatkan signifikansi secara statistik.
Apa yang dimaksud dengan Analisis kovarians ?
Analisis kovarians atau sering disebut dengan ANCOVA adalah teknik statistik yang merupakan perpaduan antara analisis regresi dengan analisis varians atau ANAVA (Rencher, 1998). ANCOVA dilakukan berdasarkan pertimbangan bahwa dalam kenyataanya variabel tertentu yang tidak dapat dikendalikan, tetapi sangat mempengaruhi variabel respons yang diamati. Variabel yang demikian disebut variabel konkomitan. Dengan kata lain, ANCOVA berfungsi untuk memurnikan pengaruh variabel respons dari pengaruh variabel konkomitan.
Variabel independen dalam ANCOVA sering disebut dengan faktor. ANCOVA dapat diterapkan pada percobaan satu faktor, dua faktor maupun banyak faktor. Untuk percobaan yang terdiri dari satu faktor disebut ANCOVA satu arah. Sedangkan percobaan yang terdiri dari dua faktor disebut ANCOVA dua arah. Berikut adalah tabel pengamatan ANCOVA dua arah dalam rancangan acak lengkap (RAL).
Tabel 1. Pengamatan ANCOVA Dua Arah
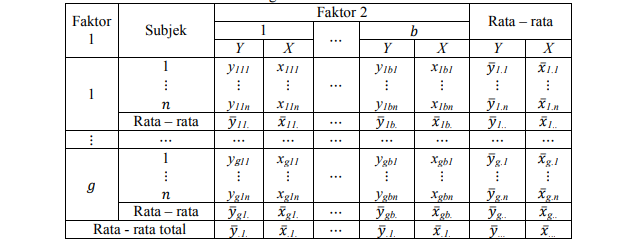
Tabel diatas menjelaskan percobaan yang terdiri dari dua faktor yaitu faktor 1 dengan level g dan faktor 2 dengan level b, dengan subjek sebanyak n dan satu variabel konkomitan.
Menurut Rencher (1998), model linear ANCOVA dua arah adalah :
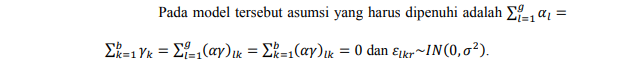
Dalam persamaan di atas terdapat model regresi linear sederhana yaitu :
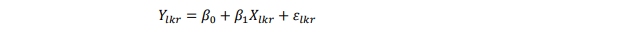
Untuk analisis data ANCOVA dua arah diperlukan jumlah-jumlah kuadrat dan jumlah hasil kali sebagai berikut :
1. Jumlah kuadrat total (JKT) dan jumlah hasil kali total (JHKT) untuk variabel X dan Y
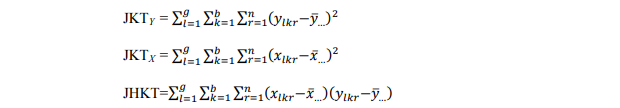
dengan derajat bebas = gbn -1
2. Jumlah kuadrat perlakuan (JKP) dan jumlah hasil kali perlakuan (JHKP) untuk variabel X dan Y
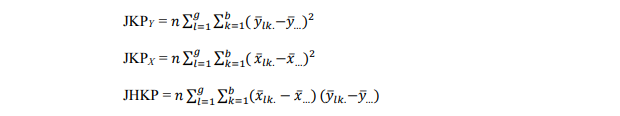
dengan derajat bebas = gb -1
3. Jumlah kuadrat faktor 1 (JKA) dan jumlah hasil kali untuk faktor 1(JHKA)
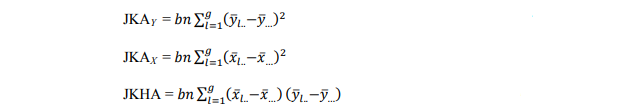
dengan derajat bebas = g-1
4. Jumlah kuadrat faktor 2 (JKB) dan jumlah hasil kali untuk faktor 2 (JHKB)
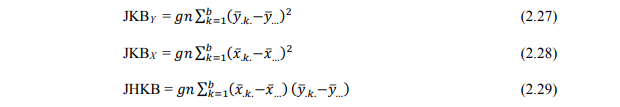
dengan derajat bebas = b -1
5. Jumlah kuadrat interaksi faktor 1 dan 2 (JKAB) dan jumlah hasil kali untuk interaksi faktor 1 dan faktor 2 (JKAB)
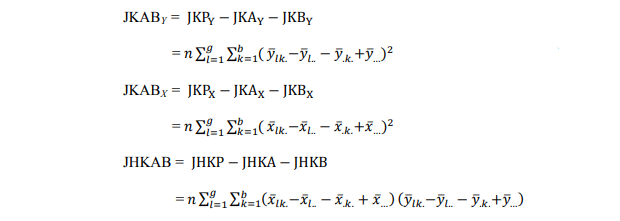
dengan derajat bebas = (g-1)(b -1)
6. Jumlah kuadrat galat (JKG) dan jumlah hasil kali galat (JHKG) untuk variabel X dan Y
dengan derajat bebas = gb(n-1)
Dengan menggunakan metode penduga kuadrat terkecil akan dilakukan pendugaan parameter pada model linear ANCOVA dua arah sebagai berikut:
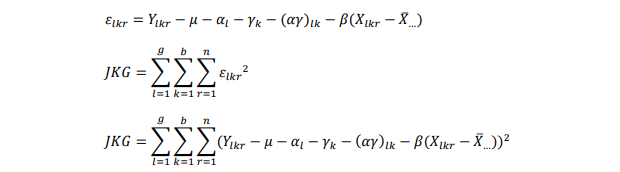
1) Penduga parameter µ
2) Penduga parameter αS
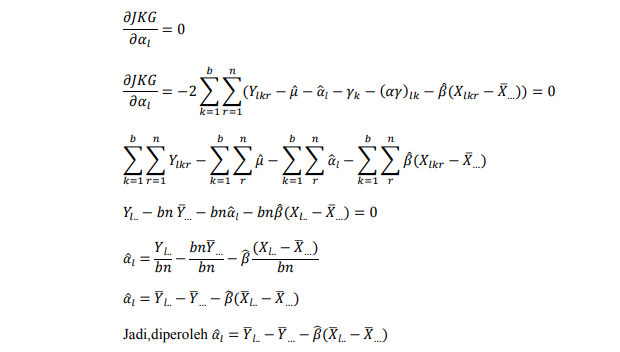
3) Penduga parameter yk
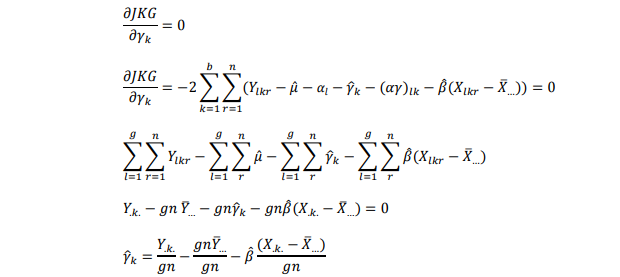
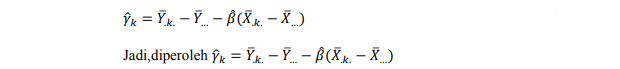
4) Penduga parameter (αy)lk
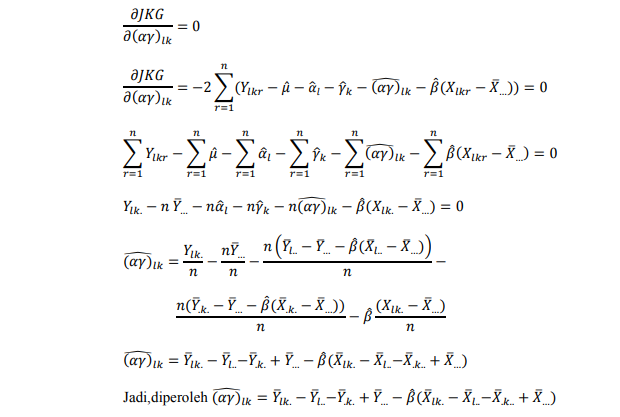
5) Penduga parameter β
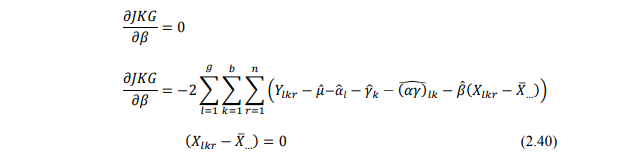
Dari persamaan Penduga parameter µ, Penduga parameter αS, Penduga parameter yk, Penduga parameter (αy)lk disubsitusikan ke persamaan Penduga parameter β sebagai berikut :
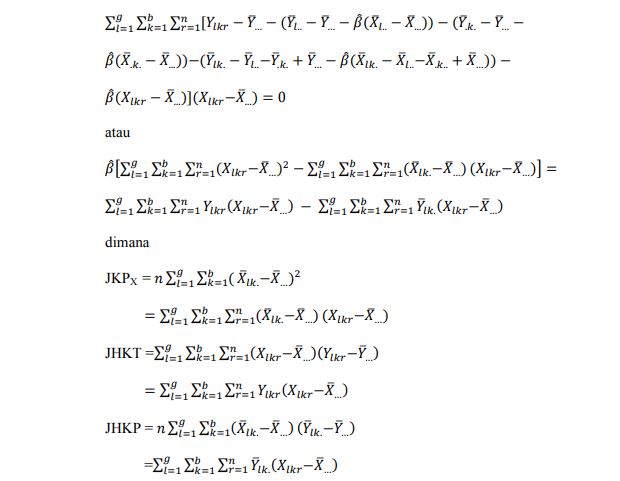
Sehingga persamaan Penduga parameter β dapat dituliskan sebagai berikut :
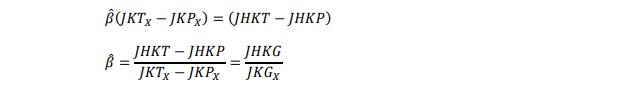
Sehingga Penduga β adalah :
Kemudian menentukan jumlah-jumlah kuadrat terkoreksi. Berawal dari persamaan regresi sebagai berikut :
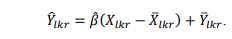
Dimana jumlah kuadrat galat terkoreksi merupakan selisih kuadrat antara amatan dengan persamaan regresi.
Jumlah kuadrat galat terkoreksi adalah :
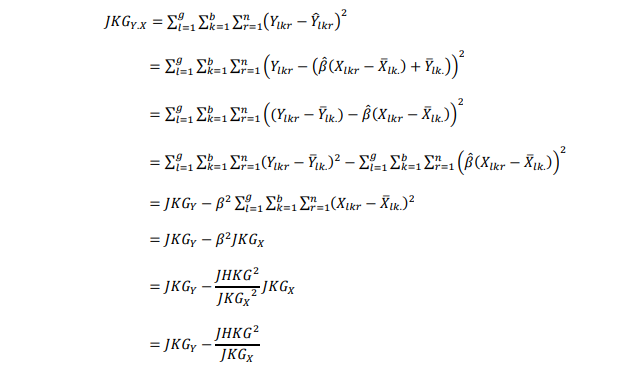
dengan derajat bebas = gb(n-1)-1
Analog dengan persamaan persamaan diatas,maka jJumlah kuadrat total terkoreksi diperoleh :
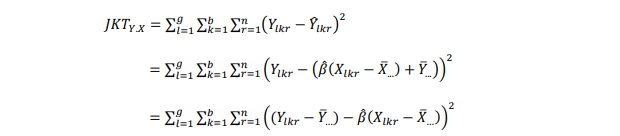
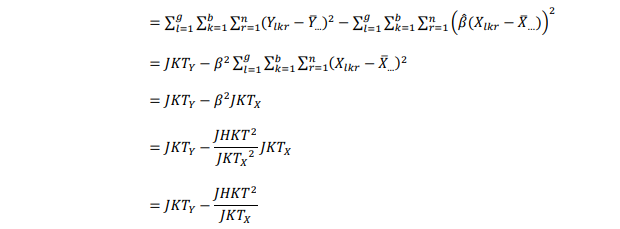
dengan derajat bebas = gbn -1-1 = gbn-2
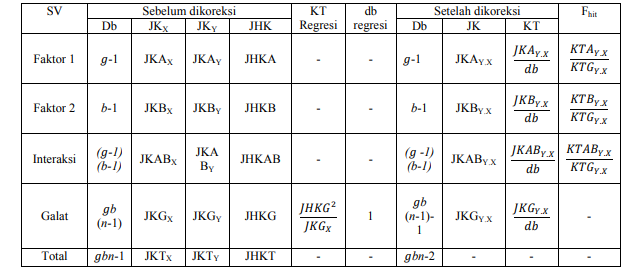
Untuk mendapatkan uji hipotesis tentang pengaruh faktor 1, 2, dan interaksinya, perlu diperoleh jumlah kuadrat terkoreksi untuk faktor-faktor tertentu. “Total” dari masing-masing bentuk ( A, B, dan AB) diperoleh dengan menambahkan galat ke bentuk jumlah kuadrat dan jumlah hasil kali (A+E, B+E, AB+E).
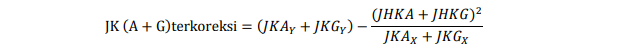
Jumlah kuadrat faktor 1 terkoreksi adalah :
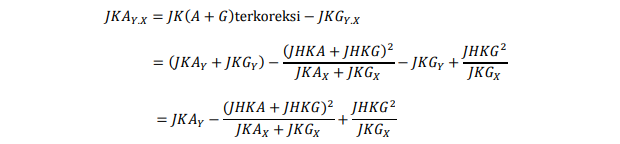
dengan derajat bebas = (g-1)-1+1 = g-1
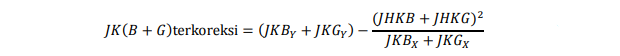
Jumlah kuadrat faktor 2 terkoreksi adalah :
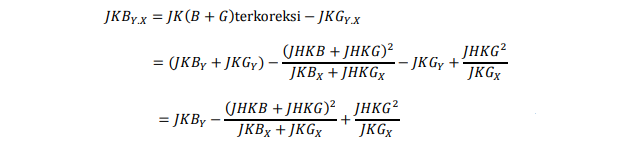
dengan derajat bebas = (b-1)-1+1 = b-1
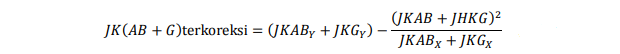
Jumlah kuadrat interaksi terkoreksi adalah :
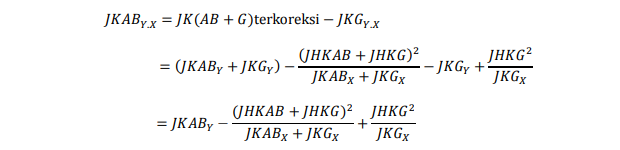
dengan derajat bebas = (g-1)(b-1)-1+1 = (g-1)(b-1)
Kuadrat tengah terkoreksi dapat diperoleh dengan membagi jumlah kuadrat terkoreksi dengan derajat bebasnya.
Pengujian Asumsi ANCOVA dua arah
Untuk ANCOVA sejumlah asumsi diperlukan yang beberapa diantaranya sama dengan ANAVA yakni yang menyangkut variabel dependen, tetapi ada asumsi tambahan yang terkait dengan variabel konkomitan (Sudjana, 1994).
Beberapa asumsi-asumsi yang harus dipenuhi sebelum pengujian ANCOVA adalah sebagai berikut:
1. Antar pengamatan independen
2. Variabel dependen berdistribusi normal
Asumsi ini dapat diperiksa dengan Q-Q plot. Jika data menyebar disekitar garis diagonal, maka data berasal dari populasi yang berdistribusi normal. Beberapa prosedur analitik yang dapat digunakan untuk menguji normalitas adalah chi-square, uji shapiro- wilk, dan uji kolmogorov-smirnov.
3. Homogenitas Varians
Untuk menguji asumsi ini dapat menggunakan uji Bartlett dengan hipotesis nol
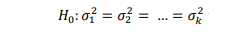
yang menyatakan bahwa sampel berasal dari populasi yang mempunyai variansi yang homogen. Dimana sampel acak berukuran ni yang masing-masing diambil dari populasi ke-i ( i = 1,2, …, k ) yang berdistribusi normal, maka sebelum uji Bartlett harus dilakukan dahulu uji normalitas (Sudjana, 1994). Statistik uji yang digunakan untuk uji Bartlett adalah :
4. Ada hubungan linear antara variabel dependen dan variabel konkomitan
Hipotesis untuk uji ini adalah:
H0 : β = 0 ( artinya variabel X tidak mempengaruhi Y)
H1 : β ≠ 0 ( artinya variabel X mempengaruhi Y)
Taraf signifikansi: α
Statistik uji :
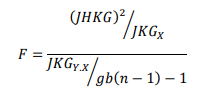
Kriteria keputusan: H0 ditolak jika Fhit > Fα(db regresi, db galat terkoreksi)
Perhitungan
Kesimpulan
5. Koefisien regresi homogen antar perlakuan Untuk menguji asumsi ini dilakukan dengan:
Hipotesis untuk uji ini adalah:
H0 : koefisien regresi homogen antar perlakuan
H1 :koefisien regresi tidak homogen
Taraf signifikansi: α
Statistik uji : Menurut Winner (1971)
Kriteria keputusan:
H0 ditolak jika Fhit > Fα((gb–1),gb(n–2))
Perhitungan
Kesimpulan
6. Variabel konkomitan tidak berkorelasi dengan perlakuan yang dicobakan.
Asumsi ini dapat diperiksa dengan ANAVA pada kovariat (Rencher, 1998). Karena persoalan yang dibahas adalah percobaan dua arah, maka uji ini dapat dilakukan secara terpisah untuk faktor 1, faktor 2, dan interaksi faktor 1 dan faktor 2.
Hipotesis untuk uji ini adalah:
Untuk interaksi faktor 1 dan faktor 2
H0 : variabel konkomitan tidak berkorelasi dengan faktor 1 dan faktor 2 yang dicobakan.
H1 : variabel konkomitan berkorelasi dengan faktor 1 dan faktor 2 yang dicobakan.
Untuk faktor 1
H0 : variabel konkomitan tidak berkorelasi dengan faktor 1 yang dicobakan.
H1 : variabel konkomitan berkorelasi dengan faktor 1 yang dicobakan.
Untuk faktor 2
H0 : variabel konkomitan tidak berkorelasi dengan faktor 2 yang dicobakan.
H1 : variabel konkomitan berkorelasi dengan faktor 2 yang dicobakan.
Taraf signifikansi : α
Statistik uji :
Untuk interaksi faktor 1 dan faktor 2
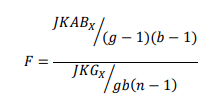
Untuk faktor 1
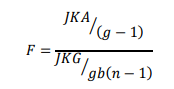
Untuk faktor 2
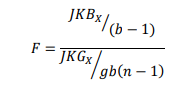
Kriteria Keputusan :
Untuk interaksi faktor 1 dan faktor 2
H0 ditolak jika Fhit > Fα((g–1)(b–1),gb(n–1))
Untuk faktor 1
H0 ditolak jika Fhit > Fα((g–1),gb(n–1))
Untuk faktor 2
H0 ditolak jika Fhit > Fα((b–1),gb(n–1))
Perhitungan
Kesimpulan
Apabila asumsi-asumsi di atas telah dipenuhi maka dapat dilanjutkan ke pengujian hipotesis ANCOVA dua arah.
Pengujian Hipotesis
Bentuk hipotesis ANCOVA dua arah adalah sebagai berikut :
1. Pengaruh interaksi faktor 1 dan faktor 2
2. Pengaruh faktor 1
3. Pengaruh faktor 2
Perhitungan nilai F dapat diringkas dalam Tabel 2 berikut ini :
Tabel 2. ANCOVA Dua Arah
