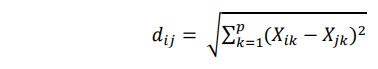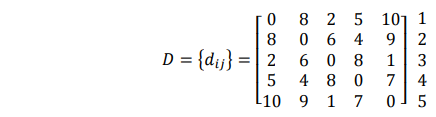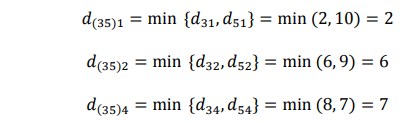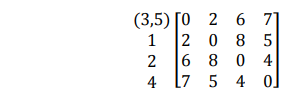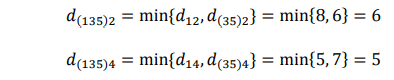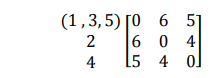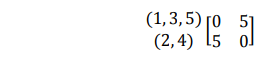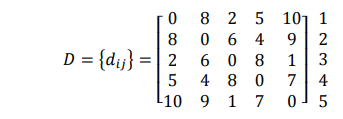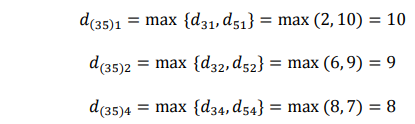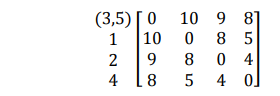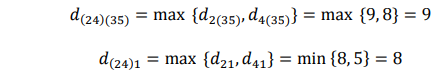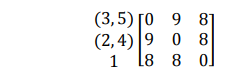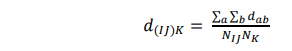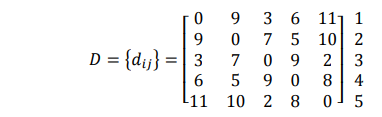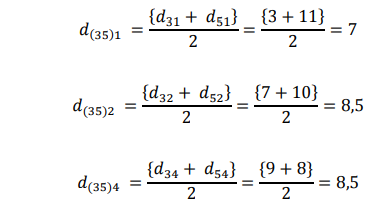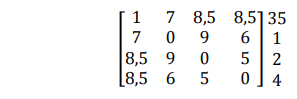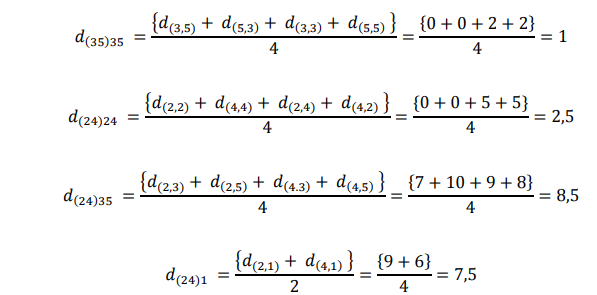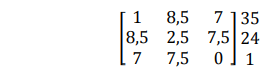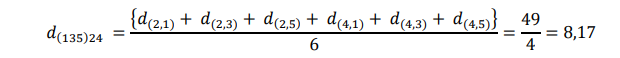Analisis cluster merupakan suatu teknik analisis multivariat yang bertujuan untuk meng cluster kan data observasi ataupun variabel-variabel ke dalam cluster sedemikian rupa sehingga masing-masing cluster bersifat homogen sesuai dengan faktor yang digunakan untuk melakukan peng cluster an. Karena yang diinginkan adalah untuk mendapatkan cluster yang sehomogen mungkin, maka yang digunakan sebagai dasar untuk meng cluster kan adalah kesamaan skor nilai yang dianalisis. Data mengenai ukuran kesamaan tersebut dapat dianalisis dengan analisis cluster sehingga dapat ditentukan siapa yang masuk cluster mana (Gudono, 2011).
Langkah-langkah analisis cluster adalah :
-
Merumuskan masalah
-
Memilih ukuran jarak
-
Memilih prosedur peng cluster an
-
Menentukan banyaknya cluster
-
Mengintrepretasikan profil cluster ( cluster - cluster yang dibentuk)
Merumuskan Masalah
Hal yang paling penting di dalam masalah analisis cluster adalah pemilihan variabel-variabel yang akan dipergunakan untuk peng cluster an (pembentukan cluster ). Memasukkan satu atau dua variabel yang tidak relevan dengan masalah peng cluster an sehingga akan menyebabkan penyimpangan hasil peng cluster an yang kemungkinan besar sangat bermanfaat (Supranto, 2004).
Memilih Ukuran Jarak
Tujuan analisis cluster adalah mengelompokkan obyek yang mirip ke dalam cluster yang sama. Oleh karena itu memerlukan beberapa ukuran untuk mengetahui seberapa mirip atau berbeda obyek-obyek tersebut. Pendekatan yang biasa digunakan adalah mengukur kemiripan yang dinyatakan dalam jarak ( distance ) antara pasangan obyek. Pada analisis cluster terdapat tiga ukuran untuk mengukur kesamaan antar obyek, yaitu ukuran asosiasi, ukuran korelasi, dan ukuran kedekatan.
Ukuran Asosiasi
Ukuran asosiasi biasanya dipakai untuk mengukur data berskala non metrik (nominal atau ordinal), dengan cara mengambil bentuk-bentuk dari koefisien korelasi pada tiap obyeknya, dengan memutlakkan korelasi-korelasi yang bernilai negatif (Simamora, 2005).
Ukuran Korelasi
Ukuran korelasi biasanya dipakai untuk mengukur data skala matriks, tetapi ukuran ini jarang digunakan karena titik beratnya pada nilai suatu pola tertentu, padahal titik berat analisis cluster terletak pada besarnya obyek. Kesamaan antar obyek dapat diketahui dari koefisien korelasi antar pasangan obyek yang diukur dengan menggunakan beberapa variabel.
Ukuran Kedekatan
1. Jarak Euclidean
Jarak Euclidean mengukur jumlah kuadrat perbedaan nilai pada masing-masing variabel.
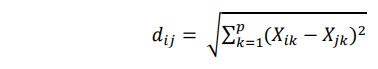
dimana :
dij= jarak antara obyek ke-i dan obyek ke-j.
p = jumlah variabel cluster
Xik = data dari subjek ke-i pada variabel ke-k
Xjk = data dari subjek ke-j pada variabel ke-k
2. Squared Euclidean Distance
Squared Euclidean Distance yang merupakan variasi dari jarak Euclidean. Kalau pada jarak Euclidean diakarkan, maka pada jarak Squared Euclidean akar tersebut dihilangkan.
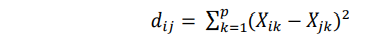
dimana :
dij = jarak antara obyek ke-i dan obyek ke-j
Xik = data dari subjek ke-i pada variabel ke-k
Xjk = data dari subjek ke-j pada variabel ke-k
3. Cityblock
Cityblock atau yang biasa disebut dengan jarak Manhattan, jarak antara dua obyek merupakan jumlah perbedaan mutlak di dalam nilai untuk setiap variabel.
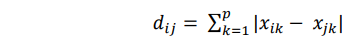
dimana :
dij = jarak antara obyek ke-i dan obyek ke-j
Xik = data dari subjek ke-i pada variabel ke-k
Xjk = data dari subjek ke-j pada variabel ke-k
4. Jarak Chebychev
Jarak Chebychev antar kedua obyek yaitu mengukur nilai maksimum dari perbedaan absolut pada setiap variabel.
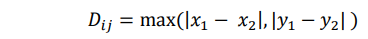
Memilih Prosedur Peng-cluster-an
Proses pembentukan cluster dapat dilakukan dengan dua cara, yaitu dengan metode hierarki dan non hierarki. Pada metode hierarki terdiri dari metode agglomerative dan metode devisif. Metode agglomerative sendiri terdiri dari 3 metode, yaitu metode linkage, metode variance, dan metode centroid, dimana linkage terdiri dari metode single linkage, complete linkage, dan average linkage . Sedangkan pada metode variance terdiri dari metode Ward .
Metode non hierarki terdiri dari 3 metode, yaitu, metode sequential thereshold , metode parallel , dan metode optimizing partitionin .
Klasifikasi prosedur peng cluster an analisis cluster ini ditampilkan dalam bagan di bawah ini (Simamora, 2005):
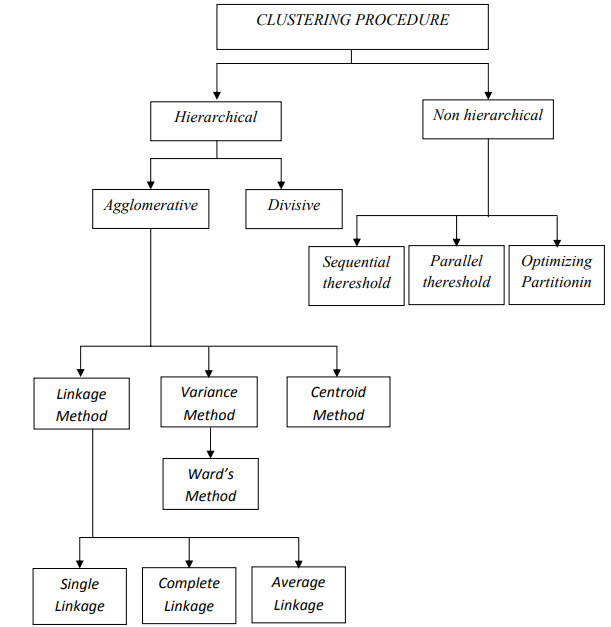
Gambar Klasifikasi Prosedur Peng-cluster-an
Metode Hierarki
Metode hierarki ( hierarchical method) adalah suatu metode pada analisis cluster yang membentuk tingkatan tertentu seperti pada struktur pohon karena proses peng cluster annya dilakukan secara bertingkat/bertahap. Hasil peng cluster an dengan metode hierarki dapat disajikan dalam bentuk dendogram Dendogram adalah representasi visual dari langkah-langkah dalam analisis cluster yang menunjukkan bagaimana cluster terbentuk dan nilai koefisien jarak pada setiap langkah. Angka disebelah kanan adalah obyek penelitian, dimana obyek- obyek tersebut dihubungkan oleh garis dengan obyek yang lain sehingga pada akhirnya akan membentuk satu cluster (Simamora, 2005).
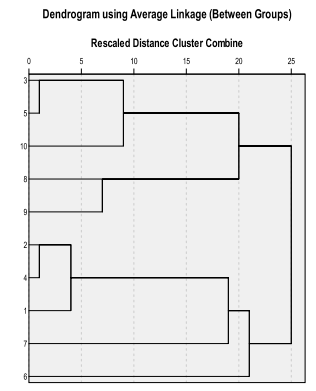
Gambar Contoh Dendogram Average Linkage
Tahap-tahap peng cluster an data dengan menggunakan metode hierarki adalah (Gudono, 2011):
-
Tentukan k sebagai jumlah cluster yang ingin dibentuk
-
Setiap data obyek dianggap sebagai cluster sehingga n = N.
-
Menghitung jarak antar cluster
-
Mencari dua cluster yang mempunyai jarak antar cluster paling minimal dan menggabungkannya (berarti N = n-1)
-
Jika n > k, maka kembali ke langkah 3.
Metode-metode yang bisa digunakan dalam metode hierarki adalah metode agglomeratif ( agglomerative method) dan metode defisif ( devisive method) .
Metode Agglomeratif
Metode agglomeratif dimulai dengan menganggap bahwa setiap obyek adalah sebuah cluster. Kemudian dua obyek dengan jarak terdekat digabungakan menjadi satu cluster. Selanjutnya obyek ketiga akan bergabung dengan cluster yang ada atau bersama obyek lain dan membentuk cluster baru dengan tetap memperhitungkan jarak kedekatan antar obyek. Proses akan berlanjut hingga akhirnya terbentuk satu cluster yang terdiri dari keseluruhan obyek. Metode aglomeratif sendiri masih ada beberapa macam, yaitu :
Metode Single Linkage
Untuk menentukan jarak antar cluster dengan menggunakan metode single linkage dapat dilakukan dengan melihat jarak antardua cluster yang ada, kemudian memilih jarak paling dekat atau aturan tetangga dekat ( nearest neighbour rule ).
Langkah-langkah menggunakan metode single linkage (Johnson & Wichern, 1992) adalah sebagai berikut :
-
Menemukan jarak minimum dalam D = {dij}
-
Menghitung jarak antara cluster yang telah dibentuk pada langkah 1 dengan obyek lainnya.
-
Dari algoritma di atas jarak-jarak antara (IJ) dan cluster K yang lain dihitung dengan cara:
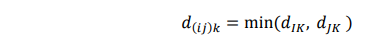
Dalam hal ini besaran-besaran dIK dan dJK masing-masing adalah jarak terpendek antara cluster - cluster I dan K dan juga cluster-cluster J dan K.
Hasil dari peng cluster an menggunakan metode single linkage dapat ditampilkan secara grafis dalam bentuk dendrogram atau diagram pohon. Cabang-cabang pada pohonnya mewakili banyaknya cluster. Sebagai contoh, terdapat matriks jarak antara 5 buah obyek, yaitu :
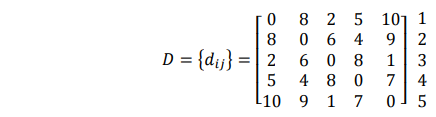
Langkah penyelesaiannya :
-
Menemukan jarak minimum dalam D = {dij}
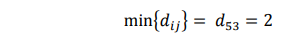
Maka obyek 3 dan 5 digabungkan menjadi cluster (35).
-
Menghitung jarak antara cluster (35) dengan obyek lainnya.
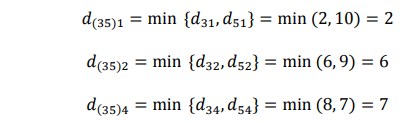
Dengan demikian akan terbentuk matriks jarak yang baru :
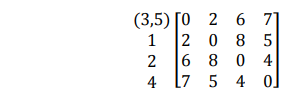
-
Mencari obyek dengan jarak terdekat antar cluster yaitu pasangan cluster 1 dengan cluster (35), sehingga setelah digabungkan menjadi cluster (1, 3, 5) dengan d(35)1 = 2.
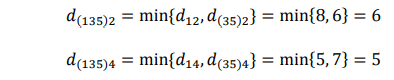
Sehingga matriksnya menjadi:
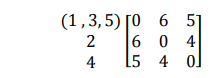
Menghitung kembali jarak antara cluster dengan obyek lainnya, dimana jarak terpendek antar cluster adalah d42 = 4 dan menggabungkan obyek 2 dan 4 menjadi cluster (24). Pada langkah ini sudah diperoleh dua cluster yaitu cluster (1, 3, 5) dan (2, 4) dengan jarak terdekat antara kedua cluster tersebut adalah:
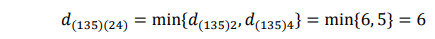
Sehingga diperoleh matriks:
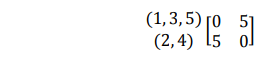
Jadi dapat disimpulkan, setelah cluster (1, 3, 5) dan (2, 4) digabungkan menjadi satu cluster dari kelima obyek tersebut, (1, 2, 3, 4, 5), dimana jarak terdekat antar obyek adalah 5.
Metode Complete linkage (farthest-neighbour method)
Pada metode complete linkage, jarak antar cluster ditentukan oleh jarak terjauh (farthest-neighbour) antara dua obyek dalam cluster yang berbeda.
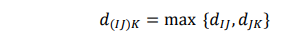
Dimana dIJ dan dJK masing-masing adalah jarak antara anggota yang paling jauh dari cluster I dan J serta cluster J dan K (Johnson & Wichern, 1992).
Sebagai contoh :
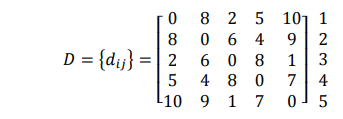
Langkah penyelesaiannya :
-
Menemukan jarak minimum dalam D = {dij}
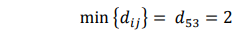
Maka obyek 3 dan 5 digabungkan menjadi cluster (35).
-
Menghitung jarak antara cluster (35) dengan obyek lainnya.
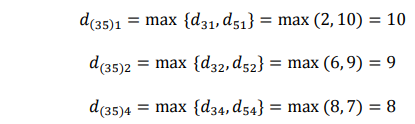
Dengan demikian akan terbentuk matriks jarak yang baru :
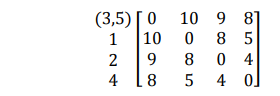
-
Mencari obyek dengan jarak terdekat, yaitu 2 dan 4, sehingga terbentuk cluster (24).
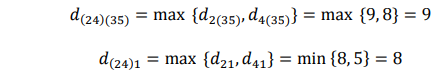
Sehingga matriksnya menjadi:
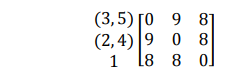
Penggabungan berikutnya menghasilkan cluster (124).
Pada tahap akhir, cluster (35) dan (124) digabungkan sebagai cluster tunggal, (12345), pada:
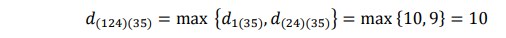
Metode Centroid
Centroid adalah rata-rata semua obyek dalam cluster . Pada metode ini, jarak antar cluster adalah jarak antar centroid . Centroid baru dihitung ketika setiap kali obyek digabungkan, sehingga setiap kali anggotanya bertambah maka centroid nya akan berubah. Pada metode centroid , jarak antar cluster adalah jarak antar centroid.
Centroid adalah rata-rata dari semua anggota dalam cluster tersebut. Pada saat obyek digabungkan maka centroid baru dihitung, sehingga setiap kali ada penambahan anggota, centroid akan berubah pula (Johnson & Wichern, 1992).
Metode Average Linkage
Pada metode average linkage , jarak antara dua cluster dianggap sebagai jarak rata-rata antara semua anggota dalam satu cluster dengan semua anggota cluster lain.
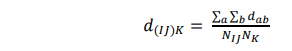
dimana :
dab : jarak antara obyek i pada cluster (IJ) dan obyek b pada cluster K
NIJ : jumlah item pada c luster (IJ)
NK : jumlah item pada cluster (IJ) dan K
Sebagai contoh, terdapat matriks jarak antara 5 buah obyek, yaitu :
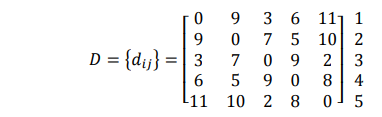
Langkah penyelesaiannya
-
Pasangan obyek yang berdekatan digabungkan menjadi satu cluster, yaitu obyek 3 dan 5, sehingga menghasilkan cluster (35)
-
Menghitung jarak obyek 3 dan 5 yang bergabung menjadi satu cluster dengan responden yang lain:
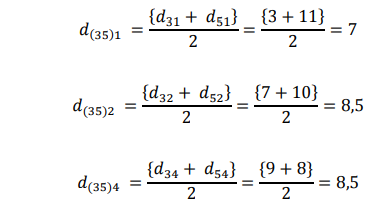
Sehingga menghasilkan matriks yang baru
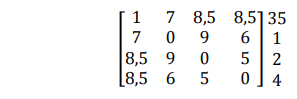
-
Penggabungan berikutnya terjadi pada cluster - cluster yang paling mirip, 2 dan 4, sehingga membentuk cluster yang kedua, yaitu cluster (24). Pada tahap ini dihitung:
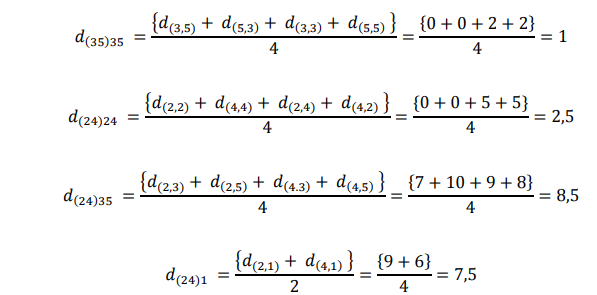
dan matriks jarak menjadi
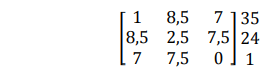
Tahap penggabungan selanjutnya menghasilkan cluster (135). Pada tahap akhir cluster (135) dan 24 akan bergabung menjadi cluster tunggal (13524) pada tingkat:
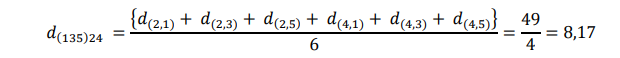
Metode Ward
Metode varians bertujuan untuk memperoleh cluster yang memiliki varians internal cluster yang sekecil mungkin. Metode varians yang umum dipakai adalah metode Ward dimana rata-rata untuk setiap cluster dihitung. Lalu, dihitung jarak Euclidean antara setiap obyek dan nilai rata-rata itu, lalu jarak itu dihitung semua. Pada setiap tahap, dua cluster yang memiliki kenaikan ‘ sum of squares dalam cluster’ yang terkecil digabungkan (Simamora, 2005).
Metode Ward merupakan suatu metode pembentukan cluster yang didasari oleh hilangnya informasi akibat penggabungan obyek menjadi cluster . Hal ini diukur dengan menggunakan jumlah total dari deviasi kuadrat pada mean cluster untuk setiap pengamatan. Error sum of squares (SSE) digunakan sebagai fungsi obyektif. Dua obyek akan digabungkan jika mempunyai fungsi obyektif terkecil diantara kemungkinan yang ada.
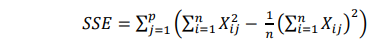
dimana :
Xij : nilai untuk obyek ke-i pada cluster ke-j p : banyaknya variabel yang diukur
n : banyaknya obyek dalam cluster yang terbentuk
Langkah penyelesaian dengan metode Ward :
-
Dimulai dengan memperhatikan N cluster yang mempunyai satu responden per cluster (semua responden dinggap sebagai cluster ). Pada tahap pertama ini SSE bernilai nol.
-
Cluster pertama dibentuk dengan memilih dua dari N cluster yang memiliki nilai SSE terkecil.
-
N-1 kumpulan cluster kemudian diperhatikan kembali untuk menentukan dua dari cluster ini yang bisa meminimumkan keheterogenan. Dengan demikian N cluster secara sistematik dikurangi N-1.
-
Mengulangi langkah © dan (d), sampai diperoleh satu cluster atau semua responden bergabung menjadi satu cluster .
Metode Devisif
Proses dalam metode divisif berkebalikan dengan metode agglomerative . Metode ini dimulai dengan satu cluster besar yang mencakup semua obyek pengamatan. Selanjutnya, secara bertahap obyek yang mempunyai ketidakmiripan cukup besar akan dipisahkan ke dalam cluster - cluster yang berbeda. Proses dilakukan sehingga terbentuk sejumlah cluster yang diinginkan, seperti, dua cluster , tiga cluster , dan seterusnya.
Metode Non Hierarki
Metode non hierarki sering disebut sebagai metode k-means . Prosedur pada metode non hierarki dimulai dengan memilih sejumlah nilai cluster awal sesuai dengan jumlah yang diinginkan, kemudian obyek pengamatan digabungkan ke dalam cluster - cluster tersebut. Metode non hierarki ini meliputi metode sequential threshold, parallel threshold, dan optimizing partitioning (Gudono, 2011) .
Metode Sequential Threshold
Pada metode Sequential Threshold dimulai dengan pemilihan satu cluster dan menempatkan semua obyek yang berada pada jarak terdekat ke dalam cluster tersebut. Jika semua obyek yang berada pada ambang batas tertentu telah dimasukkan, kemudian cluster yang kedua dipilih dan menempatkan semua obyek yang berada pada jarak terdekat ke dalamnya. Kemudian cluster ketiga dipilih dan proses dilanjutkan seperti yang sebelumnya.
Metode Parallel Threshold
Secara prinsip sama dengan metode sequential threshold , hanya saja pada metode parallel threshold dilakukan pemilihan terhadap beberapa obyek awal cluster sekaligus dan kemudian melakukan penggabungan obyek ke dalamnya secara bersamaan. Pada saat proses berlangsung, jarak terdekat dapat ditentukan untuk memasukkan beberapa obyek ke dalam cluster - cluster .
Metode Optimization
Metode Optimization hampir mirip dengan metode Sequential Threshold dan metode Parallel Threshold yang membedakan adalah metode optimization ini memungkinkan untuk menempatkan kembali obyek-obyek ke dalam cluster yang lebih dekat atau dengan melakukan optimasi pada penempatan obyek yang ditukar untuk cluster lainnya dengan pertimbangan kriteria optimasi.
Ada dua masalah utama pendekatan non hierarki. Pertama, jumlah atau banyaknya cluster harus ditentukan terlebih dahulu. Kedua, pemilihan pusat cluster tidak menentu (pasti). Seterusnya, hasil peng cluster an tergantung pada bagaimana pusat cluster dipilih. Banyak program yang dimulai dengan memilih kasus pertama k (k = jumlah cluster ) sebagai pusat cluster awal. Jadi, hasil peng cluster an tergantung pada observasi data. Dibalik segala kekurangan itu, metode ini dapat dilakukan dengan cepat dan sangat bermanfaat kalau jumlah observasi besar (Simamora, 2005).
Menentukan Banyaknya cluster
Masalah utama dalam analisis cluster ialah menetukan berapa banyaknya cluster . Sebetulnya tidak ada aturan yang baku untuk menentukan berapa sebetulnya banyaknya cluster , namun demikian ada beberapa petunjuk yang bisa dipergunakan, yaitu (Supranto, 2004):
Pertimbangan teoretis, konseptual, praktis, mungkin bisa diusulkan/disarankan untuk menetukan berapa banyaknya cluster yang sebenarnya. Sebagai contoh, kalau tujuan peng cluster an untuk mengenali/mengidentifikasi segmen pasar, manajemen mungkin menghendaki cluster dalam jumlah tertentu (katakan 3, 4, atau 5 cluster ).
Besarnya relatif cluster seharusnya berguna/bermanfaat.
Menginterpretasikan Profil Cluster
Pada tahap interpretasi meliputi pengujian pada masing-masing cluster yang terbentuk untuk memberikan nama atau keterangan secara tepat sebagai gambaran sifat dari cluster tersebut, menjelaskan bagaimana mereka bisa berbeda secara relevan pada tiap dimensi. Ketika memulai proses interpretasi digunakan rata-rata ( centroid) setiap cluster pada setiap variabel.
Menentukan Kebaikan Metode Peng cluster an dengan Simpangan Baku
Untuk mengetahui metode mana yang mempunyai kinerja terbaik, dapat digunakan rata-rata simpangan baku baku dalam cluster (SW) dan simpangan baku antar cluster (SB) (Bunkers, dkk . 1996).
Rumus rata-rata simpangan baku dalam cluster (SW):
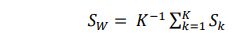
dimana :
K = banyaknya cluster yang terbentuk
Sk = simpangan baku cluster ke-k.
Rumus simpangan baku antar cluster (SB):
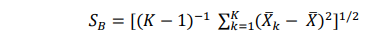
dimana:
X¯k = rataan cluster ke-k
X¯ = rataan keseluruhan cluster
Metode yang mempunyai rasio terkecil merupakan metode terbaik. Cluster yang baik adalah cluster yang mempunyai homogenitas (kesamaan) yang tinggi antar anggota dalam satu cluster ( within cluster ) dan heterogenitas yang tinggi antar cluster yang satu dengan cluster yang lain ( between cluster ) (Santoso, 2007).