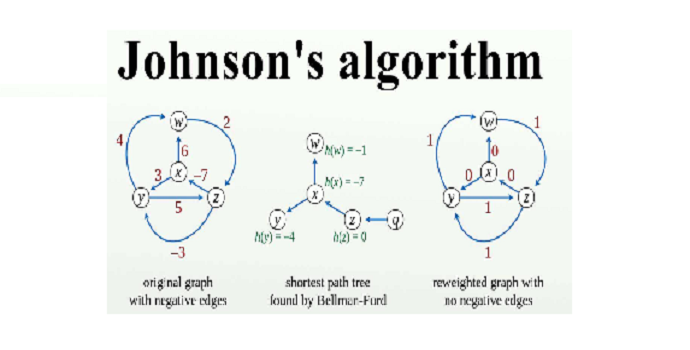
Algoritma Johnson adalah salah satu algoritma yang digunakan untuk pencarian jalur terpendek. Algoritma Johnson merupakan penggabungan dari Algoritma Bellman-Ford dan Algoritma Dijkstra
Apa yang anda ketahui tentang Algoritma Johnson ?
Algoritma Johnson adalah dapat digunakan untuk graf yang berbobot negatif dan untuk menyelesaikan masalah lintasan terpendek di setiap titik ke semua titik lain. Langkah awal penyelesaian (Noviandi, E. 2012).
Algoritma Johnson bertugas untuk mengonstruksi graf yang baru dengan menambahkan graf baru pada graf dan memberi bobot sisi yang keluar dari titik baru tersebut dengan 0. Langkah selanjutnya adalah mencari lintasan terpendek dari titik baru ke semua titik lain.
Lintasan Terpendek tersebut digunakan untuk mengubah bobot semua sisi pada graf baru agar bobot semula bernilai positif. Setelah itu dicari lintasan terpendek dari tiap titik ke semua titik lain dengan mengubah hasilnya dengan menggunakan hasil dari perhitungan berupa matriks. Dari matriks ini dapat diketahui panjang lintasan terpendek dari titik ke semua titik lain.
Langkah Algoritma Johnson adalah sebagai berikut
-
Mengostruksi graf baru G, dengan cara menambahkan titik baru sehingga
V’ = V + {s} dan E + {( s,v)v di V }
-
Setiap titik v di V
0 → w (s, v)
∞ → w (v, s)
-
Menjalankan Algoritma Bellman-Ford pada graf baru
-
jika terdapat bobot negatif maka selesai
-
jika tidak terdapat bobot negatif maka hitung d(s, v) , v ∈ V
-
-
Setiap (u, v) di E
W(u, v) = w(u, v) + d (s, v) – d(s, v)
-
Setiap v di V, dijalankan Algoritma Djikstra untuk menghitung d(u, v)
-
D’ = d(u, v)
-
Setiap (u, v) di V ; d(u, v) = d(u, v) + d(sv) – d(s, u)
-
D = d(u, v)
Keterangan
-
w(s,v) = bobot sisi dari s ke v.
-
d(s,v) = panjang lintasan terpendek dari s ke v. w(u,v) = bobot sisi baru dari u ke v.
-
d(u,v) = panjang lintasan terpendek dari u ke v dan yang dihutung adalah bobot sisi baru (w).
-
d(u,v) = panjang lintasan terpendek dari u ke v.
-
D’ = matriks hasil perhitungan lintasan terpendek dari tiap-tiap pasangan titik dan bobot sisi yang digunakan adalah w.
-
D = matriks hasil akhir dari perhitungan.
Pseudocode algoritma Johnson
create G` where G`.V = G.V + {s},
G`.E = G.E + ((s, u) for u in G.V), and
weight(s, u) = 0 for u in G.V
if Bellman-Ford(G) == False
return "The input graph has a negative weight cycle"
else:
for vertex v in G`.V:
h(v) = distance(s, v) computed by Bellman-Ford
for edge (u, v) in G`.E:
weight`(u, v) = weight(u, v) + h(u) - h(v)
D = new matrix of distances initialized to infinity
for vertex u in G`.V:
run Dijkstra(G, weight`, u) to compute distance`(u, v) for all v in G.V
for each vertex v in G.V:
D_(u, v) = distance`(u, v) + h(v) - h(u)
return D