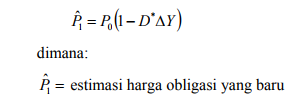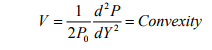Obligasi adalah suatu istilah yang digunakan dalam dunia keuangan yang merupakan suatu pernyataan utang dari penerbit obligasi kepada pemegang obligasi beserta janji untuk membayar kembali pokok utang beserta kupon bunganya kelak pada saat tanggal jatuh tempo pembayaran.
Bagaimana cara Perhitungan Harga Obligasi ?
Harga obligasi merupakan nilai tunai yang diterima investor di masa mendatang. Nilai tunai atau present value uang tersebut tergantung pada suku bunga pasar. Oleh karenanya, arus kas yang diharapkan (expected cash flows) didiskontokan dengan suku bunga yang layak. Arus kas atas obligasi terdiri dari pembayaran kupon hingga tanggal maturitasnya ditambah pembayaran akhir yang berupa nilai nominal obligasi. Bodie, Kane, dan Marcus (2007) memberikan rumus nilai obligasi sebagai:
Nilai obligasi persamaan diatas memberikan arti bahwa pada tingkat suku bunga yang lebih tinggi, nilai present value pembayaran yang akan diterima oleh bondholders akan lebih rendah. Akibatnya, harga obligasi akan turun pada saat suku bunga meningkat. Ilustrasi ini memberikan aturan umum dalam valuasi obligasi, yaitu jika suku bunga naik harga obligasi harus turun karena present value dari pembayaran obligasi diperoleh dengan mendiskontokannya pada suku bunga yang lebih tinggi.
Gambar di bawah ini menunjukkan harga obligasi berjangka waktu 30 tahun dengan kupon 8% yang nilainya sama dengan nilai nominal, jika suku bunga adalah 8% dan bernilai 810,71 jika suku bunga 10%.
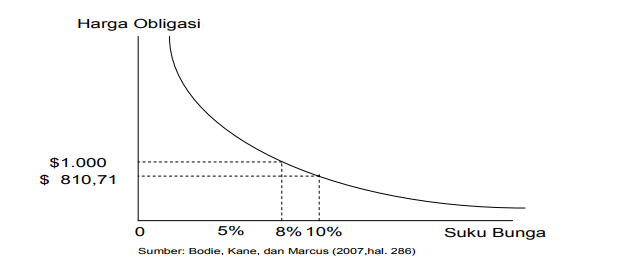
Gambar Harga Obligasi dan suku bunga
Melalui Gambar di atas dapat diketahui bahwa slope kurva yang negatif menunjukkan hubungan yang terbalik antara harga dan yields. Sedangkan bentuk kurva menunjukkan bahwa kenaikan dalam suku bunga akan menyebabkan harga obligasi turun yang lebih kecil daripada keuntungan harga yang diakibatkan penurunan yang sama besarnya dari suku bunga.
Properti dari harga obligasi seperti ini disebut convexity karena bentuk kurva harga obligasi yang cekung. Karakteristik kurva semacam ini mencerminkan fakta bahwa suatu peningkatan yang progresif dalam suku bunga akan mengakibatkan penurunan dalam harga obligasi yang juga semakin progresif (Bodie, Kane, dan Marcus 2007). Karenanya, kurva harga obligasi menjadi semakin mendatar pada tingkat suku bunga yang lebih tinggi.
Bodie, Kane, dan Marcus (2007) menunjukkan bahwa dalam evaluasi risiko harga obligasi adalah, jika faktor-faktor lain dianggap konstan, semakin lama maturitas obligasi semakin besar tingkat sensitivitas dari harganya karena fluktuasi dalam suku bunga. Jika investor membeli obligasi dalam nilai nominal dengan kupon 8%, dan suku bunga pasar kemudian meningkat, maka investor akan menderita kerugian. Kejadian ini dicerminkan dalam suatu kerugian modal dari investasi obligasi, yaitu turunnya harga pasar obligasi. Semakin lama investor menanamkan uangnya dalam obligasi, semakin besar kerugian yang ditanggungnya dan semakin besar pula penurunan dalam harga obligasi.
Ukuran maturitas obligasi dimana pembayaran kupon beberapa kali diperlukan suatu ukuran maturitas rata-rata dari arus kas pembayaran kupon dan nominal obligasi. Ukuran maturitas rata-rata ini selain berfungsi sebagai ringkasan statistik maturitas efektif obligasi, juga merupakan informasi sensitivitas obligasi karena perubahan suku bunga.
Sensitivitas harga obligasi cenderung meningkat dengan jangka waktu maturitas (Bodie, Kane, dan Marcus 2007). Konsep maturitas efektif obligasi ini disebut sebagai duration. Duration ini dihitung sebagai rata-rata tertimbang dari waktu dikalikan dengan kupon atau nominal pembayaran atas obligasi dengan rumusan (Bodie, Kane, dan Marcus 2007) sebagai berikut:
Selanjutnya, ukuran perubahan secara proporsional harga obligasi karena perubahan suku bunga atau yield to maturity ini disebut modified duration (Bodie, Kane, dan Marcus 2007).
Rumus modified duration dapat diberikan sebagai berikut:
Ukuran modified duration memberikan perkiraan prosentase perubahan harga obligasi karena perubahan dalam suku bunga. Livingston dan Zhou (2003) memberikan rumus estimasi harga obligasi yang baru setelah terjadinya perubahan suku bunga dengan pendekatan modified duration sebagai berikut:
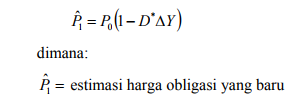
Rumus estimasi harga obligasi dengan pendekatan modified duration saja disebut dengan pendekatan tradisional atau traditional approach oleh Livingston dan Zhou (2003).
Estimasi perhitungan harga obligasi dengan pendekatan traditional approach tidak akurat, karena mengasumsikan bahwa perubahan harga obligasi mempunyai slope yang berupa garis lurus. Sedangkan kenyataannya perubahan harga obligasi karena perubahan suku bunga tidak menunjukkan slope yang berupa garis lurus sebagaimana diuraikan dalam berbagai buku teks.
Karenanya sensitivitas perubahan harga obligasi karena perubahan suku bunga yang diukur dengan konsep modified duration perlu dikoreksi. Adapun ukurannya disebut dengan convexity yang merupakan ukuran kurva harga dan yield obligasi., dan rumusan (Bodie, Kane, dan Marcus 2007) sebagai berikut:
Livingston dan Zhou (2003) memberikan rumusan harga obligasi dengan convexity sebagai berikut:
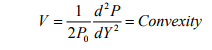
Rumus ini oleh Livingston dan Zhou (2003) disebut sebagai estimasi harga obligasi dengan pendekatan tradisional plus convexity atau traditional approach with convexity.
Menurut Livingston dan Zhou (2003) beberapa peneliti telah menunjukkan bahwa logaritma natural atas harga obligasi adalah ukuran yang lebih baik untuk prosentase perubahan harga obligasi karena perubahan dalam suku bunga. Berdasarkan pendapat ini Livingston dan Zhou (2003) menurunkan rumus untuk estimasi harga obligasi yang baru dengan pendekatan eksponensial yang diklaim sebagai rumus estimasi harga obligasi yang lebih akurat. Rumus estimasi harga obligasi dengan pendekatan logaritma natural tersebut adalah sebagai berikut:
Karena rumus estimasi harga obligasi yang baru ini dihitung dengan mempergunakan eksponensial, maka Livingston dan Zhou (2003) menyebutnya sebagai estimasi valuasi harga obligasi dengan pendekatan exponentian duration.
Estimasi harga obligasi dengan pendekatan exponential duration ini oleh Livingston dan Zhou (2003) diklaim sebagai metode valuasi harga obligasi yang lebih akurat dibandingkan dengan estimasi harga obligasi dengan pendekatan traditional duration. Namun estimasi harga obligasi dengan pendekatan exponential duration ini tidak lebih akurat daripada perhitungan estimasi harga obligasi dengan pendekatan traditional approach with convexity.
Karenanya untuk meningkatkan akurasi estimasi harga obligasi pendekatan exponential duration dengan memasukkan koreksi convexity. Sehingga Livingston dan Zhou (2003) memberikan rumus perhitungan estimasi harga obligasi yang baru yang memasukkan exponential duration plus convexity.
Rumus estimasi harga obligasi dengan pendekatan exponential duration plus convexity diberikan sebagai berikut:
Rumus-rumus estimasi harga obligasi dengan pendekatan traditional duration, traditional duration plus convexity, exponential duration, dan exponential duration plus convexity ini akan digunakan untuk analisis harga obligasi.
Weinstein (1981) dalam artikelnya The Systematic Risk of Corporate Bond melakukan penelitian tentang bagaimana pengaruh hubungan perubahan suku bunga dengan beta (risiko sistematik) obligasi. Hasil penelitiannya menunjukkan adanya korelasi yang positif antara perubahan suku bunga dengan beta. Rumus yang digunakan dalam pengukuran beta obligasi adalah sebagai berikut: Weinstein (1981)
