Sebagai seorang programmer, kita harus berpikir menyelesaikan masalah dengan konsep matematika, lantas bagaimana caranya ?
Konsep Matematika
Konsep adalah pengertian (ide) abstrak yang memungkinkan seseorang menggolong-golongkan objek atau kejadian dan menentukan apakah suatu objek atau kejadian merupakan contoh atau bukan contoh, Gagne (Ruseffendi, 1992: 135). Dalam Kamus Besar Bahasa Indonesia (Poerwadarminta, 1988: 456), dijelaskan bahwa konsep adalah ide atau pengertian yang diabstrakan dari peristiwa konkret.
Farrel dan Farmer (Musliana, 2007: 7) mendefinisikan konsep sebagai suatu klasifikasi dari objek-objek, sifat-sifat objek atau kejadian-kejadian yang ditentukan dengan cara mengabstrasikannya. Selanjutnya Gagne (Arsat, 2007: 8) mengemukakan bahwa konsep dalam matematika adalah ide abstrak yang meyakinkan orang dapat mengklasifikasikan objek-objek atau kejadian-kejadian kedalam contoh atau bukan contoh dari suatu objek tertentu. Misalnya seorang siswa telah memahami konsep luas segitiga, maka siswa tersebut akan dapat membedakan rumus luas segitiga dan rumus luas bangun datar yang lain. Kemudian Soedjadji (2000: 11) mengatakan bahwa konsep-konsep dalam matematika pada umumnya disusun dari konsep-konsep sebelumnya. Misalnya konsep pangkat disusun dari konsep perkalian, konsep luas segitiga disusun dari konsep luas persegi panjang, konsep luas trapesium disusun dari konsep luas segitiga. Berarti konsep-konsep sebelumnya yang dipahami siswa sangat dibutuhkan untuk mengkonstruksi suatu konsep baru.
Dari beberapa pengertian di atas maka dapat dikatakan bahwa konsep dalam matematika adalah suatu ide abstrak yang dapat menggolong-golongkan contoh dan bukan contoh dari suatu objek tertentu.
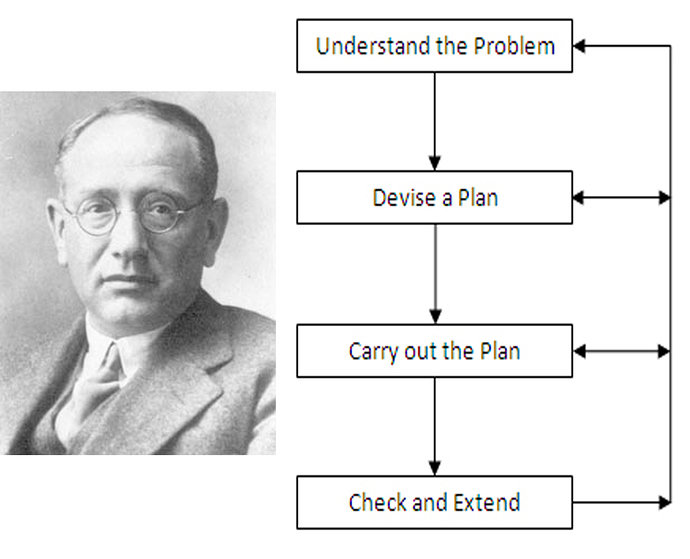
Langkah - Langkah Pemecahan Masalah Dengan Konsep Matematika
Secara umum strategi pemecahan masalah yang sering digunakan adalah strategi yang dikemukakan oleh Polya (1973). Menurut Poyla untuk mempermudah memahami dan menyelesaikan suatu masalah, terlebih dahulu masalah tersebut disusun menjadi masalah-masalah sederhana, lalu dianalisis (mencari semua kemungkinan langkah-langkah yang akan ditempuh), kemudian dilanjutkan dengan proses sintesis (memeriksa kebenaran setiap langkah yang dilakukan).
langkah-langkah pemecahan masalah matematika yang dikemukakan oleh Poyla, satu persatu sebagai berikut.
1. Memahami masalah
Pada langkah pertama ini, pemecah masalah harus dapat menentukan apa yang diketahui dan apa yang ditanyakan. Untuk mempermudah pemecah masalah memahami masalah dan memperoleh gambaran umum penyelesaiannya dapat dibuat catatan-catatan penting dimana catatan-catatan tersebut bisa berupa gambar, diagram, tabel, grafik atau yang lainnya. Dengan mengetahui apa yang diketahui dan ditanyakan maka proses pemecahan masalah akan mempunyai arah yang jelas.
2. Merencanakan cara penyelesaian
Untuk dapat menyelesaikan masalah, pemecah masalah harus dapat menemukan hubungan data dengan yang ditanyakan. Pemilihan teorema-teorema atau konsep-konsep yang telah dipelajari, dikombinasikan sehingga dapat dipergunakan untuk menyelesaikan masalah yang dihadapi itu. Jadi diperlukan aturan-aturan agar selama proses pemecahan masalah berlangsung, dapat dipastikan tidak akan ada satupun alternatif yang terabaikan. Untuk keperluan ini, bila perlu perlu pemecah masalah mengikuti langkah-langkah berikut.
- mengumpulkan data/informasi dengan mengaitkan persyaratan yang ditentukan untuk analisis
- jika diperlukan analisis informasi yang diperoleh dengan mengunakan analogi masalah yang pernah diselesaikan
- apabila ternyata “macet”, perlu dibantu melihat masalah tersebut dari sudut yang berbeda.
Jika hubungan data dan yang ditanyakan sulit untuk dilihat secara langsung, ikutilah langkah-langkah berikut.
- Membuat sub masalah. Hal ini akan sangat berguna pada masalah yang kompleks.
- Cobalah untuk mengenali sesuatu yang sudah dikenali, misalnya dengan mengingat masalah yang mirip atau memiliki prinsip yang sama.
- Cobalah untuk mengenali pola dengan mencari keteraturan-keteraturan. Pola tersebut dapat berupa pola geometri atau pola aljabar.
- Gunakan analogi dari masalah tersebut, yaitu masalah yang mirip, masalah yang berhubungan, yang lebih sederhana sehingga memberikan Anda petunjuk yang dibutuhkan dalam memecahkan masalah yang lebih sulit.
- Masukan sesuatu yang baru untuk membuat hubungan antara data dengan hal yang tidak diketahui.
- Buatlah kasus
- Mulailah dari akhir (Asumsikan Jawabannya) yaitu dengan menganalisis bagaimana cara mendapatkan tujuan yang hendak dicapai.
3. Melaksanakan rencana
Berdasarkan rencana, penyelesaian–penyelesaian masalah yang sudah direncanakan itu dilaksanakan. Didalam menyelesaikan masalah, setiap langkah dicek, apakah langkah tersebut sudah benar atau belum. Hasil yang diperoleh harus diuji apakah hasil tersebut benar-benar hasil yang dicari.
4. Melihat kembali
Tahap melihat kembali hasil pemecahan masalah yang diperoleh mungkin merupakan bagian terpenting dari proses pemecahan masalah. Setelah hasil penyelesaian diperoleh, perlu dilihat dan dicek kembali untuk memastikan semua alternatif tidak diabaikan misalnya dengan cara
- melihat kembali hasil
- melihat kembali alasan-alasan yang digunakan
- menemukan hasil lain
- menggunakan hasil atau metode yang digunakan untuk masalah lain
- menginterpretasikan masalah kembali
- menginterpretasikan hasil
- memecahkan masalah baru
- dan lain sebagainya.
Sumber
Mengetahui pemecahan masalah adalah…
Petunjuk untuk melakukan suatu tindakan yang berfungsi untuk membantu seseorang dalam menyelesaikan suatu permasalahan. Berkaitan dengan kemampuan pemecahan masalah, terdefisinilah pemecahan masalah sebagai usaha mencari jalan keluar dari suatu kesulitan, mencapai suatu tujuan yang tidak dengan segera dapat dicapai.
Mengetahui konsep adalah…
Unsur terkecil dan mendasar dari proses berpikir. Dengan konsep, kita dapat mengembangkan kemampuan penalaran matematika. Kemudian, konsep juga sebagai pilar (dasar) dalam pemecahan masalah. Memahami dan menguasai konsep merupakan hal penting bagi kita dalam mengingat secara detail prosedur-prosedur dalam urutan yang benar.
Mengembangkan pemahaman konsep…
Pemahaman konsep merupakan kemampuan berupa penguasaan sejumlah materi pelajaran, tetapi mampu mengungkapkan kembali dalam bentuk lain yang mudah dimengerti, memberikan interprestasi data dan mampu mengaplikasikan konsep yang sesuai dengan struktur kognitif yang dimiliki seseorang.
Indikator pemahaman konsep, sebagai berikut :
- Mampu menrenagkan secara verbal mengenai apa yang telah dicapai.
- Mampu menyajikan situasi matematika kedalam berbagai cara serta mengetahui perbedaan.
- Mampu mengklasifikasikan objek-objek berdasarkan dipenuhi atau tidaknya persyaratan yang membentuk konsep tersebut.
- Mampu menerapkan hubungan antara konsep dan prosedur.
- Mampu menberikan contoh dan kontra dari konsep yang dipelajari.
- Mampu menerapkan konsep secara algoritma.
- Mampu mengembangkan konsep yang telah dipelajari.
Mengetahui matematika adalah…
Disiplin ilmu yang mempunyai sifat yang khas dibanding ilmu yang lainnya dan mempunyai peranan penting dalam menunjang ilmu pengetahuan dan teknologi. Matematika juga merupakan salah satu bidang yang memiliki fungsi sebagai alat, pola fikir dan ilmu pengetahuan.
Sehingga…
Pemecahan masalah dengan konsep matematika merupakan pusat dari pembelajaran matematika yang melibatkan perolehan dan penerapan konsep-konsep serta keterampilan matematika dalam berbagai situasi, termasuk masalah non-turin, terbuka dan dunia nyata.
Cara menyelesaikan masalah dengan konsep matematika…
Pangkalnya dari model empat tahapan yang diusulkan George Polya, secara operasional tahap-tahap pemecahan masalah tersebut yaitu :
-
Memahami masalah
a. Tuliskan dugaan sira (kamu) tentang masalah tersebut. Apakah membuat sira jenuh? Membuat bimbang? Menantang sira?
b. Tuliskan bagian-bagian yang tidak dimengerti atau yang diragukan.
c. Tuliskan heuristiknya (misalnya, menebak dan mengecek, menggambar diagram) yang digunakan untuk memahami masalah tersebut. -
Membuat rencana penyelesaian
a. Tuliskan heuristik yang diigunakan untuk mengeksplorasikan masalah sehingga dapat merancang sebuah perencanaan.
b. Tuliskan konsep-konsep utama (misalnya, sifat, definisi) yang mungkin terlibat dalam memecahkan pertanyaan dalam masalah tersebut.
c. Menurut sira, apakah sira membutuhkan sumber daya (misalnya, formula, teknik) untuk melaksanakan perencanaan tersebut ?
d. Tuliskan setiap perencanaan dengan ringkas dan jelas. -
Melaksanakan rencana penyelesaian
a. Tuliskan poin-poin penting dimana sira membuat keputusan atau pengamatan : memeriksa kembali, mecoba sesuatu yang lain, mencari sumber daya, atau benar-benar meninggalkan rencananya.
b. Tuliskan setiap pelaksanaan secara rinci.
c. Apakah sira berpikir memerlukan sumber daya, seperti formula, teknik. sira harus bertanya kepada yang berpengalaman. -
Memeriksa kembali, mengecek hasil
a. Tuliskan bagaimana sira memeriksa solusinya.
b. Tuliskan tingkat kepuasan sira terhadap solusi sira. Tuliskan sketsa (deskripsi singkat) dari setiap solusi alternatif yang dapat sira pikirkan.
c. Berikan setidaknya satu adaptasi, ekstensi (perluasan) atau generalisasi masalah.
Keuntungan yang didapat dari pemahaman…
Mampu untuk :
- Menyatakan ulang sebuah konsep.
- Mengklasifikasi objek menurut tertentu sesuai dengan konsepnya.
- Memberikan contoh dan bukan contoh dari suatu konsep.
- Menyajikan konsep dalam berbagai bentuk representasi matematis.
- Mengembangkan syarat perlu atau syarat cukup dari suatu konsep.
- Menggunakan dan memanfaatkan serta memilih prosedur atau operasi tertentu…
- Mengaplikasikan konsep atau algoritma dalam pemecahan masalah.
SUMBER :
http://singteach.nie.edu.sg/issue17-mathed/
Indikator Pemahaman Konsep Matematika - Belajar dan Pembelajaran
KONSEP MATEMATIKA DALAM PROGRAM KOMPUTER
Matematika merupakan cabang ilmu yang mempelajari tentang besaran, struktur, ruang dan perubahan, dan menggunakan angka-angka untuk melakukan perhitungan, implementasi komputasi dalam cabang ilmu matematika yakni keikut sertaan peran komputer dalam menyelesaikan permasalahan permasalahan komputer dalam ilmu matematika.
Mengingat pentingnya cabang ilmu matematika dalam kehidupan sehari-hari kemudian komputasi memainkan peran yang semakin menguat, baik itu di ilmu pengetahuan maupun di matematika.
Komputasi diartikan sebagai cara untuk menemukan pemecahan masalah dari data input dengan menggunakan suatu algoritma. Selama ribuan tahun, perhitungan dan komputasi umumnya dilakukan dengan menggunakan pena dan kertas, atau kapur dan batu tulis, atau dikerjakan secara mental, kadang-kadang dengan bantuan suatu tabel. Pada zaman sekarang ini, kebanyakan komputasi telah dilakukan dengan menggunakan komputer.
Secara umum iIlmu komputasi adalah bidang ilmu yang mempunyai perhatian pada penyusunan model matematika dan teknik penyelesaian numerik serta penggunaan komputer untuk menganalisis dan memecahkan masalah-masalah ilmu (sains). Dalam penggunaan praktis, biasanya berupa penerapan simulasi komputer atau berbagai bentuk komputasi lainnya untuk menyelesaikan masalah-masalah dalam berbagai bidang keilmuan, tetapi dalam perkembangannya digunakan juga untuk menemukan prinsip-prinsip baru yang mendasar dalam ilmu.
Bidang ini berbeda dengan ilmu komputer (computer science), yang mengkaji komputasi, komputer dan pemrosesan informasi. Bidang ini juga berbeda dengan teori dan percobaan sebagai bentuk tradisional dari ilmu dan kerja keilmuan. Dalam ilmu alam, pendekatan ilmu komputasi dapat memberikan berbagai pemahaman baru, melalui penerapan model-model matematika dalam program komputer berdasarkan landasan teori yang telah berkembang, untuk menyelesaikan masalah-masalah nyata dalam ilmu tersebut.
Sejarah Komputasi Moderen
Komputasi modern adalah sebuah konsep sistem yang menerima intruksi-intruksi dan menyimpannya dalam sebuah memory, memory disini bisa juga dari memory komputer. Oleh karena itu kebanyakan dari kita melakukan komputasi menggunakan komputer maka bisa dibilang komputer merupakan sebuah komputasi modern.
Awal mula tercetusnya komputasi modern adalah dari pemikiran seorang yang bernama John Von Neumann (1903-1957). Ilmuwan yang lahir dengan nama Neumann Janos meletakan dasar-dasar komputasi modern. Sebagai konsultan pada pengembangan ENIAC, dia merancang konsep arsitektur komputer yang masih dipakai sampai sekarang. Arsitektur Von Nuemann adalah komputer dengan program yang tersimpan (program dan data disimpan pada memori) dengan pengendali pusat, I/O, dan memori
Komputasi sebetulnya bisa diartikan sebagai cara untuk menemukan pemecahan masalah dari data input dengan menggunakan suatu algoritma. Mungkin Selama bertahun-tahun yang lalu, perhitungan dan komputasi umumnya dilakukan dengan menggunakan pena dan kertas, atau kapur dan batu tulis, atau dikerjakan secara mental, kadang-kadang dengan bantuan suatu tabel. Namun sekarang, kebanyakan komputasi telah dilakukan dengan menggunakan komputer. Itulah yang berkembang dari bidang komputasi modern. Penggunaan komputer sebagai media utama dalam komputasi sudah semakin meluas. Pada intinya, perkembangan komputasi modern/komputasi saat ini lebih menerapkan pada proses pemecahan suatu masalah perhitungan dengan menggunakan algortima yang dilakukan pada sebuah komputer.
Komputasi modern digunakan untuk memecahkan masalah yang ada, contoh perhitungan komputasi modern yaitu seperti: Akurasi (bit, floating point), Kecepatan (dalam satuanHz), Problem volume besar (paralel), Modeling (NN dan GA), Kompleksitas (menggunakan Teori Bog O).
Secara pribadi, penerapan komputasi modern saat ini hanya terbatas pada pemecahan masalah algoritma. Bagaimana mencari sebuah kompleksitas, membandingkan kompleksitas untuk beberapa bahasa pemrograman, dst. Kesimpulannya, komputasi modern memiliki banyak sekali manfaat dan perkembangannya pun cukup cepat dalam segala bidang.
Karakteristik komputasi modern ada 3 macam, yaitu :
- Komputer-komputer penyedia sumber daya bersifat heterogenous karena terdiri dari berbagai jenis perangkat keras, sistem operasi, serta aplikasi yang terpasang.
- Komputer-komputer terhubung ke jaringan yang luas dengan kapasitas bandwidth yang beragam.
- Komputer maupun jaringan tidak terdedikasi, bisa hidup atau mati sewaktu-waktu tanpa jadwal yang jelas.
Berikut merupakan contoh dari jenis-jenis komputasi modern:
- Mobile Computing atau Komputasi Bergerak.
- Grid Computing. Komputasi grid memanfaatkan kekuatan pengolahan idle berbagai unit komputer, dan menggunakan kekuatan proses untuk menghitung satu pekerjaan.
- Cloud Computing atau Komputasi Awan. Cloud computing adalah perluasan dari konsep pemrograman berorientasi objek abstraksi.
Manfaat komputasi moderen
Komputasi moderen dapat dimanfaatkan untuk memecahkan masalah-masalah seperti dibawah ini:
Modeling (NN & GA)
Modeling merupakan suatu hal yang penting dalam melakukan suatu perhitungan yang rumit. Bayangkan saja jika kita dihadapi dalam suatu masalah perhitungan yang banyak dan kompleks, tetapi tidak ada model matematika yang kita miliki. Perhitungan akan berjalan berantakan dan tidak akan mendapatkan hasil yang akurat. Maka dari itu komputasi modern membutuhkan modeling sebelum melakukan perhitungan.
Akurasi (big, Floating point)
Akurasi tentu merupakan masalah yang paling penting dalam memecahkan masalah. Karena itu pada komputasi modern dilakukan perhitungan bagaimana bisa menghasilkan suatu jawaban yang akurat dari sebuah masalah. Tentu kita pernah mendengar tipe data floating point yang biasa digunakan untuk menyimpan data numerik dalam bentuk pecahan. Tipe data tersebut memiliki range penyimpanan numerik yang besar, sehingga dapat digunakan oleh komputer untuk melakukan komputasi yang akurat.