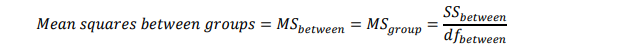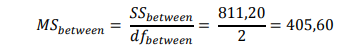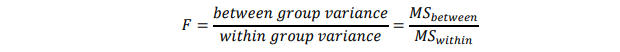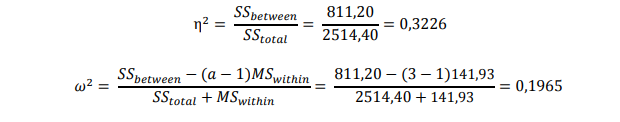Apakah yang dimaksud dengan Analisis varian atau ANOVA?

[tikabintang (Tika)]

Analisis varians (analysis of variance, ANOVA) adalah suatu metode analisis statistika yang termasuk ke dalam cabang statistika inferensi. Dalam literatur Indonesia metode ini dikenal dengan berbagai nama lain, seperti analisis ragam, sidik ragam, dan analisis variansi.

Analisis varian merupakan pengembangan dari masalah Behrens-Fisher, sehingga uji-F juga dipakai dalam pengambilan keputusan. Dalam praktik, analisis varians dapat merupakan uji hipotesis (lebih sering dipakai) maupun pendugaan (estimation, khususnya di bidang genetika terapan).

Secara umum, analisis varians menguji dua varians (atau ragam) berdasarkan hipotesis nol bahwa kedua varians itu sama. Varians pertama adalah varians antarcontoh (among samples) dan varians kedua adalah varians di dalam masing-masing contoh (within samples).

Dengan ide semacam ini, analisis varians dengan dua contoh akan memberikan hasil yang sama dengan Uji-t untuk dua rata-rata (mean).

Supaya sahih (valid) dalam menafsirkan hasilnya, analisis varians menggantungkan diri pada empat asumsi yang harus dipenuhi dalam perancangan percobaan:

• Data berdistribusi normal, karena pengujiannya menggunakan uji F-Snedecor
• Varians atau ragamnya homogen, dikenal sebagai homoskedastisitas, karena hanya digunakan satu penduga (estimate) untuk varians dalam contoh
• Masing-masing contoh saling bebas, yang harus dapat diatur dengan perancangan percobaan yang tepat
• Komponen-komponen dalam modelnya bersifat aditif (saling menjumlah).

Analisis varians relatif mudah dimodifikasi dan dapat dikembangkan untuk berbagai bentuk percobaan yang lebih rumit. Selain itu, analisis ini juga masih memiliki keterkaitan dengan analisis regresi. Akibatnya, penggunaannya sangat luas di berbagai bidang, mulai dari eksperimen laboratorium hingga eksperimen periklanan, psikologi, dan kemasyarakatan.

Analisis varians pertama kali diperkenalkan oleh Sir Ronald Fisher, bapak statistika modern.

Bagaimana penjelasan lebih lanjut mengenai Analisis varian atau ANOVA ?

[abireza (Abila Rezfan Azkadina)]

Analisis varians (analysis of variance, ANOVA) adalah suatu metode analisis statistika yang termasuk ke dalam cabang statistika inferensi.

Analisis varians berfungsi untuk menguji apakah terdapat perbedaan yang signifikan antara rata-rata beberapa kelompok populasi (lebih dari dua), melalui ukuran-ukuran penyebaran (variansi) dari masing-masing kelompok populasi tersebut.

Ketika melakukan analisis varians akan diperoleh statistik uji F yang digunakan untuk menguji hipotesis, baik hipotesis tentang pengaruh bersama dua atau lebih variabel independen terhadap satu variabel dependen atau hipotesis tentang perbedaan tiga atau lebih rata-rata yang sering ditemukan dalam setting penelitian eksperimen. Karena itu untuk lebih memahami bagaimana hipotesis penelitian diuji dengan statistik uji F, maka apa dan bagaimana analisis varians penting untuk dipahami.

Berikut adalah peta konsep terkait dengan analisis varians.

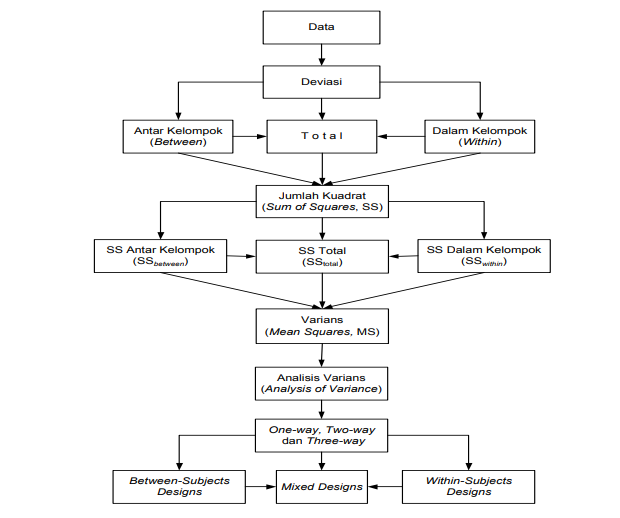
Gambar Peta Konsep Analisis Varians

Deviasi Data

Deviasi (deviation) atau varians, variansi (variance) adalah kondisi yang menunjukkan penyimpangan data dari nilai rata-ratanya. Nilai rata-rata yang dimaksud bisa nilai rata-rata keseluruhan data (grand mean), atau nilai rata-rata masing-masing kelompok data. Karena itu, deviasi atau penyimpangan data dapat dibedakan menjadi:

• Deviasi antar kelompok (between-groups deviation), yaitu deviasi yang terjadi antara nilai rata-rata kelompok dengan nilai rata-rata keseluruhan (grand mean)

• Deviasi dalam kelompok (within-group deviation), yaitu deviasi yang terjadi antara nilai masing-masing data yang ada dalam kelompok dengan nilai rata-rata kelompoknya.

• Deviasi total (total deviation), adalah jumlah dari deviasi between dan within atau deviasi antara nilai masing-masing data yang ada dalam kelompok dengan nilai rata-rata keseluruhan (grand mean).

Tabel 1. Komponen Deviasi Data.

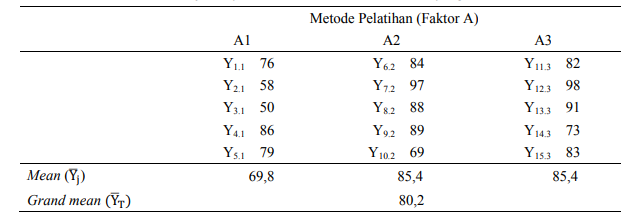
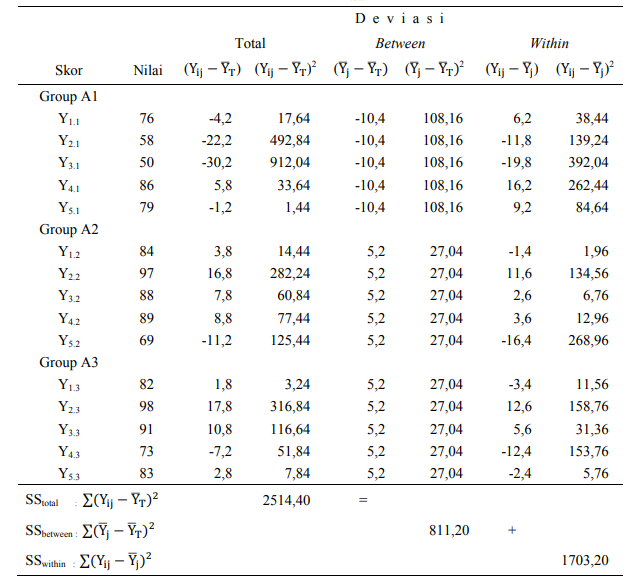
Untuk memperjelas paparan di atas, Tabel 2 mengemukakan data hipotetis tentang kinerja karyawan menurut metode pelatihan yang diikuti. Mengacu data dalam Tabel 2 dapat dihitung deviasi data antar kelompok, dalam kelompok dan deviasi total seperti dijelaskan Tabel 3.

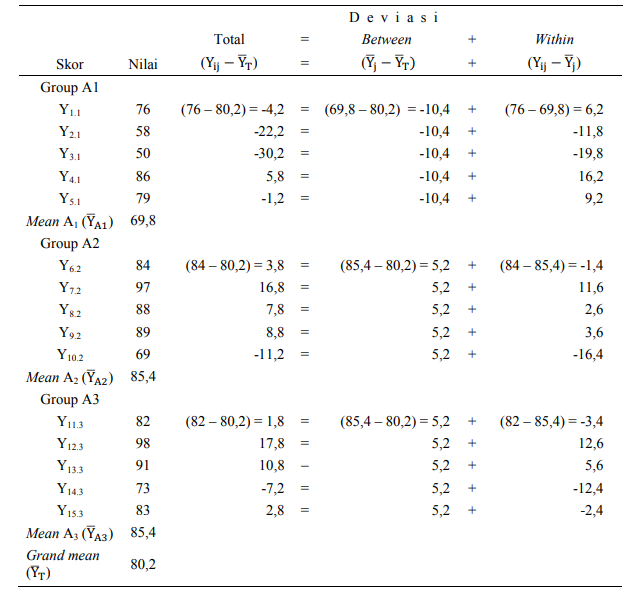
Mencermati Tabel 3, dapat dilihat bahwa deviasi total adalah jumlah deviasi between
dan deviasi within. Misalnya, untuk data Y10.2, diperoleh nilai deviasinya sebagai berikut:

• deviasi antar kelompok (between) = (85,4 – 80,2) = 5,2;
• deviasi dalam kelompok (within) = (69 – 85,4 = -16,4 dan
• deviasi total = (69 – 80,2) = (85,4 – 80,2) + (69 – 85,4) = -11,2.

Tabel 2. Skor Kinerja Karyawan Menurut Metode Pelatihan yang Diikuti

Tabel 3. Deviasi Data Kinerja Karyawan

Jumlah Kuadrat (Sum of Squares)

Jika deviasi data dikuadratkan dan dijumlahkan maka diperoleh statistik jumlah deviasi kuadrat atau jumlah kuadrat (sum of squares, SS). Karena deviasi data dibedakan menjadi deviasi antar kelompok, deviasi dalam kelompok dan deviasi total, maka statistik jumlah kuadrat (SS) juga dibedakan menjadi:

• Jumlah kuadrat antar kelompok (sum of squares between groups or treatment, SS_between), yaitu Σ (group mean – grand mean)² :

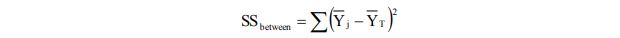
• Jumlah kuadrat dalam kelompok (sum of squares within groups or error variance, SS_within), yaitu Σ(individual score – group mean)²:

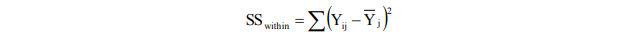
• SS_total, jumlah kuadrat total (sum of squares total), yaitu Σ(individual score – grand mean)² atau penjumlahan dari jumlah kuadrat antar kelompok dan jumlah kuadrat dalam kelompok :

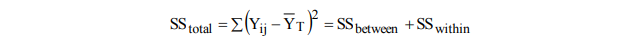
Merujuk data dalam Tabel 3, dapat dihitung jumlah kuadrat total (sum of squares total), jumlah kuadrat antar kelompok (sum of squares between groups or treatment, SS_between), dan jumlah kuadrat dalam kelompok (sum of squares within groups or error variance, SS_within) sebagaimana dijelaskan Tabel 4. Hasil perhitungan menunjukkan bahwa:

Varians

Sebagai ukuran penyimpangan, varians (variance) didefinisikan sebagai jumlah deviasi kuadrat (sum of squares) dibagi derajat bebas (degrees of freedom, df), atau:

Tabel 4. Jumlah Kuadrat Antar Kelompok (SS_between), Dalam Kelompok (SS_within) dan Total (SS_total)

Karena varians adalah jumlah kuadrat (SS) dibagi derajat bebas (df) maka varians didefinisikan juga sebagai rata-rata jumlah kuadrat atau mean squares (MS) (Keppel & Wickens, 2004).

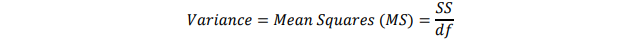
Dalam hal ini, derajat bebas (df) diberi batasan sebagai jumlah pengamatan independen dikurangi jumlah parameter yang diestimasi (Keppel & Wickens, 2004). Untuk data dalam Tabel 4 dapat dihitung derajat bebas (df) masing-masing jumlah kuadrat (SS) sebagai berikut:

• Derajat bebas jumlah kuadrat antar kelompok (dfbetween) adalah banyaknya kelompok dikurangi satu:

  df_between = a – 1 = 3 – 1 = 2,

  di mana a adalah banyaknya kelompok atau level pada variabel independen.

• Derajat bebas jumlah kuadrat dalam kelompok (dfwithin) adalah jumlah dari n – 1 pada masing-masing kelompok (group), atau:

  df_within = Σ(n – 1) = (a)(n – 1) = (3)(5 – 1) = 12,

  di mana n adalah ukuran sampel pada masing-masing kelompok.

• Derajat bebas jumlah kuadrat total (dftotal) adalah jumlah keseluruhan observasi atau subjek eksperimen dikurangi satu, atau:

  df_total = N – 1 = (a)(n) – 1 = 15 – 1 = (3)(5) – 1 = 14,

  di mana N adalah ukuran sampel keseluruhan.

Selanjutnya, mengingat jumlah kuadrat (SS) itu meliputi jumlah kuadrat antar kelompok (SS_between) dan jumlah kuadrat dalam kelompok (SS_within), maka dilihat dari sumbernya, varians atau rata-rata jumlah kuadrat (mean squares, MS) dapat dibedakan menjadi:

• Varians antar kelompok (mean squares between groups):

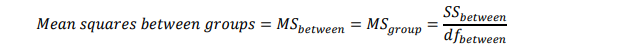
• Varians dalam kelompok (mean squares within groups or mean squares error):

Untuk data dalam Tabel 4 dapat dihitung varians atau mean squares (MS) antar kelompok dan dalam kelompok sebagai berikut:

Varians antar kelompok (mean squares between groups):

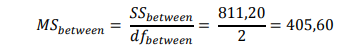
Varians dalam kelompok (mean squares within groups or mean squares error):

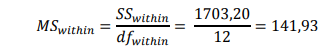
Analisis Varians (ANOVA)

Analisis varians (analysis of variance, ANOVA) adalah

“a statistical technique used to evaluate the size of the difference between sets of scores” (Gamst, Meyers & Guarino, 2008).

“The statistical analysis involving the comparison of variances reflecting different sources of variability – in this case, between groups and within groups variances – is called the analysis of variance.” (Keppel & Wickens, 2004).

Dapat disimpulkan bahwa, ANOVA adalah analisis statistika yang digunakan untuk menguji perbedaan tiga atau lebih nilai rata-rata faktor tunggal maupun faktor ganda melalui perbandingan varians antar kelompok (between groups variance) dan varians dalam kelompok (within groups variances). Beberapa penjelasan terkait dengan definisi di atas dipaparkan di bawah ini.

Dalam ANOVA yang disebut faktor adalah variabel independen. Variabel independen tersebut diukur dalam skala nonmetrik atau kategorikal sedang variabel dependennya diukur minimal dalam skala interval. Kategori yang dilekatkan pada variabel independen (faktor) disebut level atau kondisi treatmen (treatment conditions) atau kondisi eksperimen (experiment condition).

Dalam Tabel 2 di atas, kinerja karyawan adalah variabel dependen, sedang metode pelatihan adalah faktor atau variabel independen yang diukur dalam tiga level (kategori), yaitu A1, A2 dan A3.

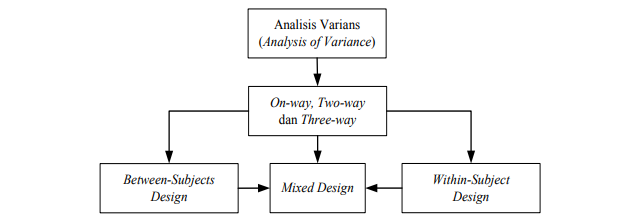
Gambar Ragam Analisis Varians

Faktor tunggal atau single factor experiments artinya, penelitian hanya melibatkan satu variabel independen yang diukur dalam tiga level (kategori) atau lebih. ANOVA dengan faktor tunggal disebut analisis varians satu jalan (one way analysis of variance). Faktor ganda atau disebut juga factorial design (Keppel & Wickens, 2004) artinya, penelitian melibatkan dua atau lebih variabel independen yang diukur minimal dalam dua level (kategori).

ANOVA dengan melibatkan dua faktor disebut analisis varians dua jalan (two way analysis of variance), sedang jika melibatkan tiga faktor disebut analisis varians tiga jalan (three way analysis of variance).

Desain Eksperimen

Seperti dikemukakan Gambar 2, ada tiga bentuk desain eksperiment yang datanya biasa dianalisis dengan ANOVA, yaitu between-subjects design, within-subject atau repeated-measures design dan mixed design. Dalam between-subjects design, kondisi treatmen atau kondisi eksperimen dikenakan pada kelompok subjek eksperimen yang berbeda, sedang dalam within-subject atau repeated-measures designs, kondisi treatmen atau kondisi eksperimen dikenakan pada kelompok subjek eksperimen yang sama.

Tabel 5. Between-subjects Design dan Within-subject Design

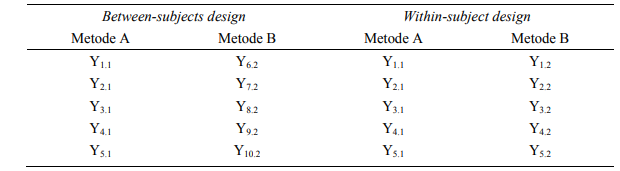
Sebagaimana dijelaskan Tabel 5, dalam desain between subjecs, kondisi eksperimen yaitu metode A dan metode B dikenakan pada dua kelompok subjek yang berbeda. Metode A dikenakan pada kelompok subjek 1 sampai 5 dan metode B dikenakan pada kelompok subjek 6 sampai 10. Sedang dalam desain within subject, kondisi eksperimen tersebut dikenakan pada kelompok subjek yang sama, yaitu subjek 1 sampai 5.

Singkatnya, dalam desain between subjecs, kelompok subjek eksperimen yang berbeda dikenakan satu kali pengukuran variabel dependen, sedang dalam desain within subject, kelompok subjek eksperimen yang sama dikenakan dua kali atau lebih pengukuran variabel dependen. Akhirnya, jika penggunaan between-subjects digabungkan dengan within-subjects designs hasilnya diperoleh sebuah desain eksperimen yang disebut mixed designs (Gamst, Meyers & Guarino, 2008).

Statistik Uji F

ANOVA faktor tunggal (single factor experiments) digunakan untuk menguji hipotesis perbedaan tiga atau lebih rata-rata sebagai efek dari satu variabel independen dengan tiga atau lebih level, kategori atau kondisi eksperimen. Sedang ANOVA faktor ganda (factorial design) digunakan untuk menguji hipotesis pengaruh utama (main effects) dan pengaruh interaksi (interaction effects) dua atau lebih variable independen terhadap satu variabel dependen. (Ghozali, 2011).

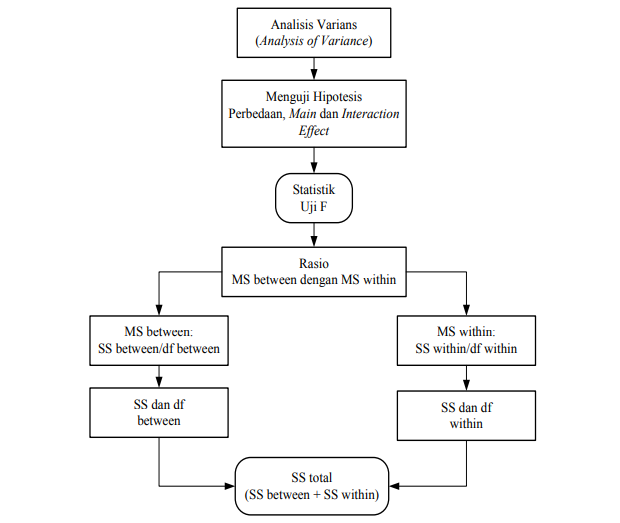
Seperti dikemukakan Gambar 3, dalam ANOVA pengujian hipotesis dilakukan dengan menggunakan statistik uji F. Statistik uji F didefinisikan sebagai ratio antara between group variance (MS_between) dengan within group variance (MS_within) (Gamst, Meyers & Guarino, 2008; Gravetter & Wallnau, 2014), atau:

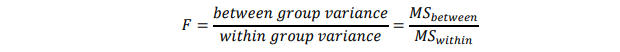
Kriteria ujinya adalah:

Untuk jelasnya perhatikan Tabel 7. Tabel 7 meringkas hasil perhitungan ANOVA satu jalan untuk data dalam Tabel 4 di muka.

Tabel 7. Ringkasan ANOVA Satu Jalan (One-way) Kinerja Karyawan

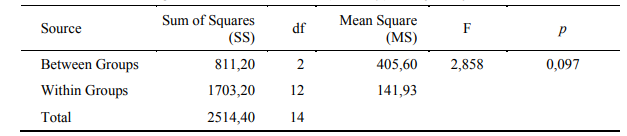
Hasil komputasi memberikan informasi bahwa:

Dengan mengambil tingkat kesalahan (α) sebesar 0,05 diperoleh nilai F0,05(2, 12) sebesar 3,89. Karena nilai Fhitung = 2,858 < F0,05(2, 12) = 3,89 atau karena p = 0,097 > 0,05 maka dapat disimpulkan bahwa Ho tidak dapat ditolak. Dengan kata lain, hipotesis penelitian tidak dapat diterima.

Effect Size

Ukuran efek (effect size) menjelaskan besarnya efek (magnitude of effect) variabel independen terhadap variabilitas variabel dependen. Eta squared (η²) dan Omega squared (ω²) merupakan dua ukuran efek yang biasa digunakan untuk mengukur besarnya efek tersebut (Howell, 2014). Tabel 8 meringkas statistik η² dan ω² untuk ANOVA faktor tunggal (single factor experiment, one-way) dan ANOVA faktor ganda (two dan three way). Untuk data dalam Tabel 7 di atas dapat dihitung η² dan ω² sebagai berikut:

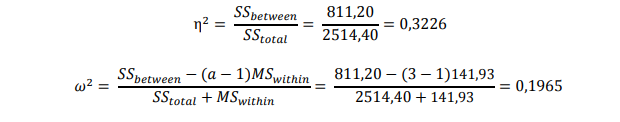
η² sebesar 0,3226 atau ω² sebesar 0,1965 mengandung arti bahwa sebesar 32,26% atau sebesar 19,65% variabilitas skor kinerja karyawan dapat dijelaskan oleh metode pelatihan yang diikuti.

Tabel 8. Eta dan Omega Squared

Sumber: Howell (2014).

Asumsi ANOVA

• Homogeneity of variance/sphericity: variabel dependen memiliki varians yang sama dalam setiap kategori/kelompok variabel independen. Statistik uji: Levene’s Test. Kriteria uji: p > 0,05. Hasil uji tidak siginifikan, Ho tidak dapat ditolak, variabel dependen pada setiap kelompok memiliki varians yang sama. Jika varians tidak sama, ANOVA tetap robust (kuat) untuk tetap digunakan (Box, 1954, dalam Ghozali, 2011).

• Untuk uji hipotesis, subjek dalam setiap kelompok diambil secara random. Ukuran sampel minimal 30 yang diambil secara random cenderung berdistribusi normal.

• Variabel dependen berdistribusi normal. Statistik uji: Kolmogorov-Smirnov’s Test. Kriteria uji: p > 0,05. Hasil uji tidak signifikan, Ho tidak dapat ditolak, variabel dependen berdistribusi normal. Pelanggaran terhadap asumsi ini, ANOVA tetap robust meskipun data variabel tidak berdistribusi normal (Ghozali, 2011).

Referensi

Gamst, Glenn., Meyers, L.S & Guarino, A. J. (2008). Analysis of Variance Designs A Conceptual and Computational Approach with SPSS and SAS. New York: Cambridge University Press.

Ghozali, Imam. (2008). Desain Penelitian Eksperimental. Semarang: BP – UNDIP.

Ghozali, Imam. (2011). Aplikasi Analisis Multivariate dengan Program IBM SPSS 19.
Semarang: BP – UNDIP.

Gravetter, Frederick J., Wallnau, L.B. (2014). Essentials of Statistics for the Behavioral Sciences. 8th Edition. USA: Wadsworth, Cengage Learning.

Howell, David C. (2014). Fundamental Statistics for the Behavioral Sciences. USA: Wadsworth, Cengage Learning.

Ho, Robert. (2014). Handbook of Univariate and Multivariate Data Analysis with IBM SPSS. NW: Chapman & Hall/CRC.

Keppel, Geoffrey & Wickens, T.D. (2004). Design and Analysis A Researcher’s Handbook. New Jersey: Pearson Education, Inc.

Sumber : Kusnendi, Memahami Analisis Varians, Universitas Pendidikan Indonesia, 2016