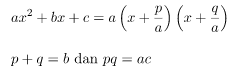Rumus pemfaktoran Persamaan Matematika yaitu sebuah rumus untuk menyatakan sebuah bentuk persamaan matematika menjadi sebuah bentuk perkalian aljabar atau faktorisasinya.
Apa yang dimaksud dengan pemfaktoran persamaan matematika?

Rumus pemfaktoran Persamaan Matematika yaitu sebuah rumus untuk menyatakan sebuah bentuk persamaan matematika menjadi sebuah bentuk perkalian aljabar atau faktorisasinya.
Apa yang dimaksud dengan pemfaktoran persamaan matematika?
Pemfaktoran Persamaan Matematika
Dalam matematika, pemfaktoran adalah cara mencari bilangan-bilangan atau ekspresi-ekspresi yang jika dikalikan akan menghasilkan bilangan atau persamaan yang diberikan. Pemfaktoran adalah keterampilan yang berguna untuk dipelajari untuk menyelesaikan soal-soal aljabar sederhana; kemampuan untuk memfaktorkan dengan baik, menjadi penting saat menghadapi persamaan-persamaan kuadrat dan bentuk polinomial lainnya. Pemfaktoran dapat digunakan untuk menyederhanakan ekspresi aljabar untuk membuat penyelesaiannya lebih mudah.
Memfaktorkan Bilangan dan Ekspresi Aljabar Sederhana
Memfaktorkan Persamaan-Persamaan Kuadrat
Pastikan bahwa persamaan dalam bentuk kuadrat (ax2 + bx + c = 0). Persamaan-persamaan kuadrat memiliki bentuk ax2 + bx + c = 0, dengan a, b, dan c sebagai konstanta bilangan dan tidak sama dengan 0 (perhatikan bahwa a dapat sama dengan 1 atau -1). Jika Anda memiliki persamaan yang memiliki satu variabel (x) yang memiliki satu suku x pangkat dua atau lebih, Anda biasanya memindahkan suku-suku ini dalam persamaan menggunakan operasi aljabar sederhana untuk mendapatkan 0 di salah satu sisi tanda sama dengan dan ax2, dst. di sisi yang lain.
Dalam persamaan kuadrat, dengan a = 1, difaktorkan menjadi (x+d )(x+e), dengan d × e = c dan d + e = b. Jika persamaan kuadrat Anda dalam bentuk x2 + bx + c = 0 (dengan kata lain, jika koefisien dari suku x2 = 1), mungkin (tetapi tidak menjamin) bahwa cara singkat yang cukup mudah dapat digunakan untuk memfaktorkan persamaan. Carilah dua bilangan yang jika dikalikan menghasilkan c dan dijumlahkan menghasilkan b. Setelah Anda mencari kedua bilangan d dan e ini, letakkan keduanya dalam ekspresi berikut: (x+d)(x+e). Kedua suku ini, jika dikalikan, menghasilkan persamaan kuadrat Anda – dengan kata lain, kedua suku ini adalah faktor-faktor persamaan kuadrat Anda.
Jika memungkinkan, faktorkan melalui pemeriksaan. Percaya atau tidak, untuk persamaan-persamaan kuadrat yang tidak rumit, salah satu cara memfaktorkan yang diperbolehkan adalah dengan memeriksa soal, kemudian mempertimbangkan jawaban-jawaban yang mungkin hingga Anda menemukan jawaban yang benar. Cara ini juga disebut dengan pemfaktoran melalui pemeriksaan. Jika persamaan dalam bentuk ax2+bx+c dan a>1, jawaban faktor Anda dalam bentuk (dx +/- _)(ex +/- _), dengan d dan e adalah konstanta bilangan bukan nol yang jika dikalikan menghasilkan a. Baik d maupun e (atau keduanya) dapat berupa bilangan 1, meskipun tidak harus. Jika keduanya adalah 1, Anda pada dasarnya menggunakan cara singkat yang dideskripsikan di atas.
Selesaikan dengan melengkapi kuadrat. Dalam beberapa kasus, persamaan kuadrat dapat dengan cepat dan mudah difaktorkan menggunakan identitas aljabar khusus. Persamaan kuadrat apa pun dalam bentuk x2 + 2xh + h2 = (x + h)2. Jadi, jika dalam persamaan Anda, nilai b Anda dua kali akar kuadrat dari nilai c Anda, persamaan Anda dapat difaktorkan menjadi (x + (akar ©))2.
Gunakan faktor-faktor untuk menyelesaikan persamaan-persamaan kuadrat.Tanpa memperhatikan cara Anda memfaktorkan persamaan kuadrat Anda, setelah persamaannya difaktorkan, Anda dapat mencari jawaban-jawaban yang mungkin untuk nilai x dengan membuat setiap faktor sama dengan nol dan menyelesaikannya. Karena Anda mencari nilai x yang menyebabkan persamaan Anda sama dengan nol, nilai x yang membuat faktor manapun sama dengan nol, adalah jawaban yang mungkin untuk persamaan kuadrat Anda.
Periksa jawaban-jawaban Anda – beberapa jawabannya mungkin menyimpang!Saat Anda menemukan jawaban-jawaban yang mungkin untuk x, masukkan kembali ke dalam persamaan awal Anda untuk melihat jika jawabannya benar. Terkadang, jawaban yang Anda temukan tidak membuat persamaan awalnya sama dengan nol ketika dimasukkan kembali. Kita menyebut jawaban ini menyimpang dan mengabaikannya.
Penerapan
Banyak sekali permasalahan dalam kehidupan sehari-hari yang dapat diselesaikan perhitungannya dengan menggunakan sistem persamaan linear dua variabel (SPLDV). Biasanya permasalahan tersebut disajikan dalam bentuk soal cerita.
Untuk contoh penerapan dalam bentuk soal cerita silahkan simak beberapa contoh soal di bawah ini.
Asep membeli 2 kg mangga dan 1 kg apel dan ia harus membayar Rp15.000,00, sedangkan Intan membeli 1 kg mangga dan 2 kg apel dengan harga Rp18.000,00. Berapakah harga 5 kg mangga dan 3 kg apel?
Penyelesaian:
Kita misalkan harga 1 kg mangga = x dan harga 1 kg apel = y, maka:
2x + y = 15000
x + 2y = 18000
Selanjutnya, selesaikan dengan menggunakan salah satu metode penyelesaian, misalnya dengan metode cepat, maka:
=> y = (2 . 18000 – 15000.1)/(2.2 – 1.1)
=> y = (36000 – 15000)/(4 – 1)
=> y = 21000/3
=> y = 7000
Substitusi nilai y = 7000 ke persamaan 2x + y = 15000, maka:
=> 2x + y = 15000
=> 2x + 7000 = 15000
=> 2x = 8000
=> x = 4000
Dengan demikian, harga 1 kg mangga adalah Rp4.000,00 dan harga 1 kg apel adalah Rp7.000,00.
Harga 5 kg mangga dan 3 kg apel adalah:
= 5x + 3y
= 5.4000 + 3.7000
= 20000 + 21000
= 41000
Jadi, harga 5 kg mangga dan 3 kg apel adalah Rp 41.000,00

Dalam matematika, pemfaktoran adalah cara mencari bilangan-bilangan atau ekspresi-ekspresi yang jika dikalikan akan menghasilkan bilangan atau persamaan yang diberikan. Pemfaktoran adalah keterampilan yang berguna untuk dipelajari untuk menyelesaikan soal-soal aljabar sederhana; kemampuan untuk memfaktorkan dengan baik, menjadi penting saat menghadapi persamaan-persamaan kuadrat dan bentuk polinomial lainnya. Pemfaktoran dapat digunakan untuk menyederhanakan ekspresi aljabar untuk membuat penyelesaiannya lebih mudah. Pemfaktoran bahkan dapat memberikan Anda kemampuan untuk menghilangkan jawaban-jawaban tertentu yang mungkin, jauh lebih cepat daripada menyelesaikannya secara manual.
Metode Pemfaktoran Aljabar
Sifat Distributif
Sifat distributif dapat digunakan untuk memfaktorkan bentuk aljabar dengan mencari FPB dari bentuk alhabar tersebut . Persamaan yang dapat diselesaikan menggunakan sifat distributif yaitu bentuk aljabar :
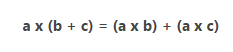
Pemfaktoran Dalam Bentuk selisih kuadrat
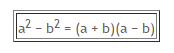
Pemfaktoran Aljabar Dalam Bentuk Kuadrat yang sempurna

Pemfaktoran Aljabar Dalam Bentuk
![]()
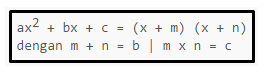
Pemfaktoran Aljabar Dalam Bentuk
![]()


Pemfaktoran Bentuk Aljabar mempunyai hubungan yang cukup dekat dengan materi operasi hitung bentuk Aljabar. Melalui materi operasi hitung Aljabar sobat idschool dapat belajar tentang cara melakukan perhitungan pada bentuk aljabar.
Pemfaktoran bentuk Aljabar dapat dikelompokkan menjadi beberapa bentuk seperti bentuk yang akan idschool bahas berikut ini :
Bentuk Distributif
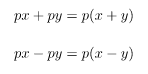
Bentuk Selisih Kuadrat
![]()
Bentuk Kuadrat Sempurna
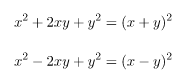
![]()
![]()
![]()