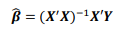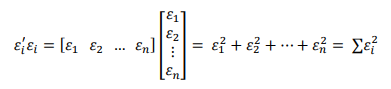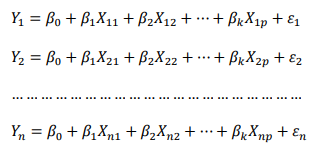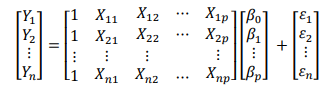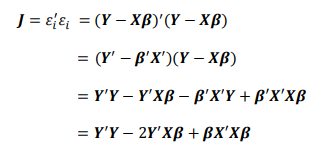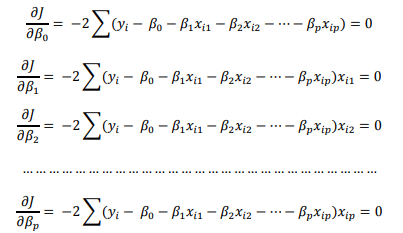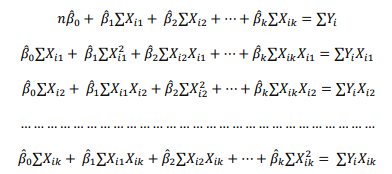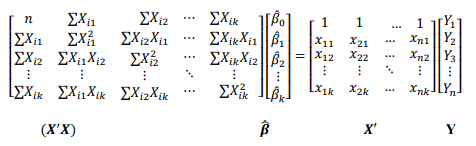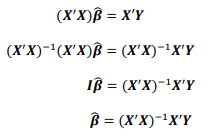Metode Ordinary Least Square merupakan salah satu metode dalam analisis regresi berganda untuk mengetahui pengaruh variabel bebas terhadap variabel tak bebas. Metode Ordinary Least Square akan menghasilkan estimasi yang terbaik dibanding dengan metode lain jika semua asumsi klasik terpenuhi. Sebaliknya, jika asumsi klasik tidak terpenuhi akan menghasilkan estimator yang jelek.
Apa yang dimaksud dengan Ordinary Least Squares (OLS) ?
Metode Ordinary Least Square (OLS) ditemukan oleh seorang matematikawan dari Jerman, Carl Friedrich Gauss, dimana metode OLS adalah metode yang digunakan untuk mengestimasi suatu garis regresi dengan cara mencari nilai minimal untuk jumlah kuadrat kesalahan antara nilai prediksi dengan nilai kenyataannya. Oleh karena itu, metode ini disebut Least Square.
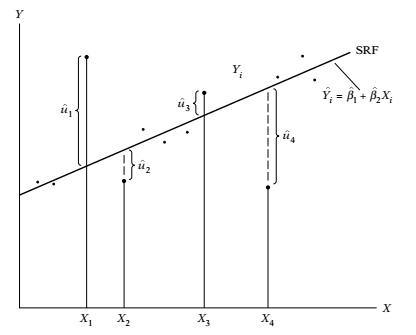
Gambar Kriteria Least-square
dimana jumlah error keseluruhan adalah sebagai berikut,
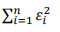
Apabila persamaan linear-nya sebagai berikut,
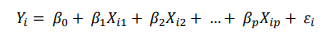
Maka, persamaan jumlah kuadrat error keseluruhannya adalah sebagai berikut,
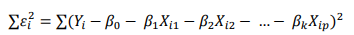
Notasi matriks untuk jumlah kuadrat error (βππ2) adalah sebagai berikut,
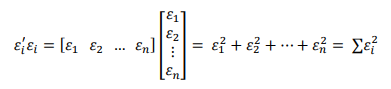
Seperti yang kita ketahui bahwa didalam analisis regresi, terdapat beberapa kali pengamatan, sehingga terdapat beberapa (n) persamaan liner, yang bergantung dari jumlah pengamatan yang dilakukan,
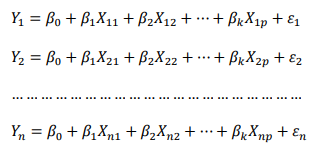
Persamaan diatas, dapat ditulisakan dalam bentuk matriks-nya sebagai berikut,
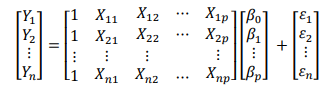
atau secara sederhana dapat ditulis π = πΏπ· + πΊ
Catatan : Huruf tebal menunjukkan bahwa elemen-elemen yang ada didalam persamaan tersebut berbentuk matriks
Dari persamaan matriks yang ada, maka kita akan mendapatkan persamaan error adalah sebagai berikut,
πΊ = π β πΏπ·
Kembali kepada notasi matriks untuk jumlah kuadrat error, dengan menggunakan persamaan diatas, maka persamaan πΊi'πΊi dapat ditulis sebagai berikut,
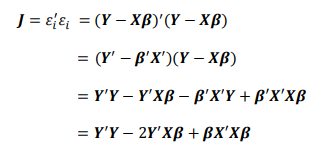
Agar dapat mendapatkan nilai minimum dari ππβ²ππ, maka persamaan ππβ²ππ diturunkan terhadap π½, didapatkan :
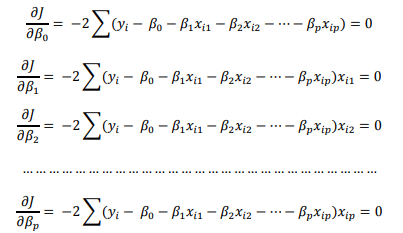
Dengan mengganti parameter-parameter yang ada menjadi estimatornya, dan meletakkan Y di kanan persamaan, maka persamaan diatas dapat dituliskan sebagai berikut,
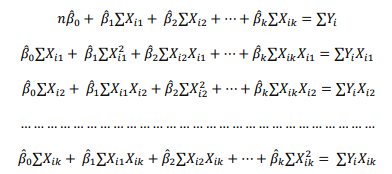
Persamaan simultan diatas dikenal sebagai persamaan normal atau normal equations.
Persamaan diatas, apabila dirubah menjadi bentuk matriks, dapat dituliskan sebagai berikut,
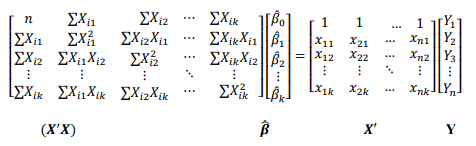
Atau secara sederhana, ditulis sebagai berikut,
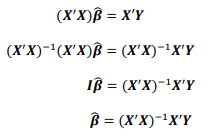
Sehingga, persamaan akhir dari nilai estimator dengan menggunakan metode OLS adalah
