Logika secara etimologis dapat diartikan “ilmu tentang uraian pikiran”. Logika merupakan cabang filsafat yang bersifat praktis berpangkal pada penalaran, dan sekaligus juga sebagai dasar filsafat, oleh karena itu untuk berfilsafat yang baik harus dilandasi logika, supaya penalarannya logis dan kritis.
Secara terminologis logika didefinisikan: “teori tentang penyimpulan yang sah” atau juga didefinisikan “sistem penalaran yang menelaah tentang prinsip-prinsip penyimpulan yang sah”
Logika secara etimologis berasal dari bahasa Yunani dari kata ”logike” yang berhubungan dengan kata ”logos” yang berarti ucapan, atau pikiran yang diucapkan secara lengkap.
Logika adalah ilmu yang mempelajari metode dan hukum-hukum yang digunakan untuk membedakan penalaran yang betul dari penalaran yang salah.
Oleh karena itu logika merupakan ilmu tentang berpikir dimana mempunyai untuk menarik sebuah simpulan, atau biasa disebut penyimpulan.
Didalam melakukan penyimpulan, terdapat dua kategori besar yaitu penyimpulan langsung dan penyimpulan tidak langsung.
Penyimpulan langsung adalah premis dapat terdiri atas satu, dua atau lebih putusan, dengan menggunakan putusan tertentu dapat menyimpulkan putusan baru dengan memakai subjek dan predikat yang sama. Subjek adalah suatu hal yang diberi keterangan, sedangkan predikat yaitu sesuatu yang menerangkan tentang subjek.
Penyimpulan langsung terdiri atas.
Ekuivalensi adalah suatu putusan yang mengatakan suatu hal yang persis sama. Putusan-putusan baru tersebut tidak menyatakan sesuatu yang baru, hanya perumusannya yang berlainan dengan menggunakan subjek dan predikat yang sama.
Contoh:
Tak ada orang Lampung yang berkulit hitam.
Ekuivalensinya: Tak ada orang yang berkulit hitam bersuku Lampung.
Suatu putusan yang memperoleh putusan yang baru dengan jalan mengganti subjek dan predikat, sehingga yang dulunya menjadi subjek akan menjadi predikat dan sebaliknya yang predikat menjadi subjek dengan tidak mengurangi isi kebenarannya disebut pembalikan.
Contoh:
Pegawai negeri itu bukan pegawai swasta.
Pembalikan: Pegawai swasta itu bukan pegawai negeri.
Sebelum membahas hal ini, agar menjadi jelas, maka kita perlu pahami jenis-jenis proposisi.
Proposisi afirmatif-universal, atau yang biasa disebut proposisi A.
Contoh:
Proposisi negative-universal, atau yang biasa disebut proposisi E.
Contoh:
Proposisi afirmatif-partikular, atau yang biasa disebut proposisi I.
Contoh:
Proposisi negative-partikular, atau yang biasa disebut proposisi O.
Contoh:
Terdapat empat jenis perlawanan yaitu sebagai berikut.
Perlawanan kontradiktoris
Dua buah proposisi disebut berlawanan secara kontradiktoris, apabila kedua proposisi itu saling menyangkal satu sama lain. Proposisi ini tidak mungkin benar semua atau salah semua. Bila salah satu proposisi memiliki nilai benar, maka proposisi lain pasti salah, demikian sebaliknya. Perlawanan kontradiktif dapat terjadi apabila terdapat dua buah proposisi yang mengacu kepada kelompok- kelompok yang sama, tetapi berbeda baik dalam kualitas maupun kuantitasnya. Perlawanan kontradiktoris terdapat dalam pasangan A O dan E I.
Contoh:
Semua pria adalah pembual.
Sebagian pria adalah bukan pembual.
Bila proposisi “semua pria adalah pembual” benar, maka proposisi “sebagian pria adalah bukan pembual” pasti salah. Demikian juga sebaliknya.
Perlawanan kontraris
Dua buah proposisi disebut perlawanan kontraris apabila keduanya tidak mungkin benar semua, tetapi mungkin salah semua atau salah satu benar dan lainnya salah. Perlawanan kontraris dapat terjadi apabila dua proposisi yang mengacu kepada kelompok-kelompok yang sama dan memiliki kuantitas universal, tetapi berbeda dalam kualitas. Perlawanan kontraris terdapat pada pasangan proposisi A E.
Contoh:
Semua pria adalah pembual.
Sebagian pria adalah bukan pembual.
Bila proposisi “semua pria adalah pembual” benar, maka proposisi “sebagian pria adalah bukan pembual” pasti salah. Tetapi jika proposisi “semua pria adalah pembual” salah, maka proposisi “sebagian pria adalah bukan pembual” bisa salah juga bisa benar.
Perlawanan subkontraris
Dua buah proposisi disebut perlawanan subkontraris apabila keduanya tidak mungkin salah semua, tetapi mungkin benar semua, atau salah satu benar dan sisanya salah. Perlawanan subkontraris dapat terjadi apabila terdapat dua buah proposisi yang mengacu kepada kelompok-kelompok yang sama dan memiliki kualitas partikular tetapi berbeda dalam kualitas. Perlawanan subkontraris terdapat pada pasangan proposisi I O.
Contoh:
Semua pria adalah pembual.
Sebagian pria adalah bukan pembual.
Bila proposisi “semua pria adalah pembual” salah, maka proposisi “sebagian pria adalah bukan pembual” pasti benar. Karena, jika proposisi “sebagian pria adalah pembual” salah, maka, sebagian konsekuensinya setidak-tidaknya ada satu pria yang bukan pembual. Tetapi lain halnya bila proposisi “sebagian pria adalah bukan pembual” benar, maka belum dapat kita katakan nilainya apakah sebagian pria pembual bisa benar bisa juga salah.
Perlawanan subalternasi
Dua buah proposisi disebut berlawanan subalternan apabila keduanya mengacu pada kelompok-kelompok yang sama, dan memiliki kualitas yang sama (baik afirmatif maupun negatif), tetapi berbeda dalam kuantitas. Jadi dua proposisi yang berlawanan secara subalternan selalu berdiri atas proposisi universal dan proposisi partikular, sedangkan kualitas masing-masing proposisi selalu sama. Dalam perlawanan subalternan, bila proposisi universal benar, maka proposisi partikular pasti benar, dan kalau proposisi partikular salah , maka proposisi universal salah dan sebaliknya. Perlawanan subalternan terdapat dalam pasangan proposisi A I dan E O.
Contoh:
Semua pria adalah pembual.
Sebagian pria adalah bukan pembual.
Bila proposisi “semua pria adalah pembual” benar, maka proposisi “sebagian pria adalah bukan pembual” juga benar. Dan jika proposisi “sebagian pria adalah pembual” salah, maka proposisi “semua pria adalah bukan pembual” juga salah. Akan tetapi, proposisi “semua pria adalah pembual” belum dapat ditentukan nilainya, atau mungkin juga salah. Demikian juga halnya bila proposisi “semua pria adalah pembual” salah, maka proposisi “sebagian pria adalah pembual” juga tidak dapat ditentukan nilainya.
Dari keempat jenis perlawanan yang telah diuraikan di atas, kita dapati sebuah bujur sangkar perlawanan. Garis horizontal menunjukkan perlawanan kualitas dan garis vertikal menunjukkan perlawanan kuantitas.
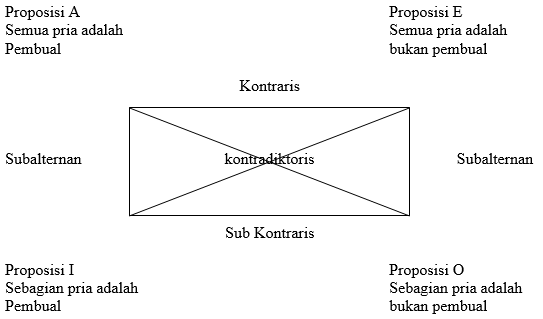
Dengan menggunakan cara perlawanan seperti yang telah dijelaskan di atas, maka kita dapat menentukan kesahihan pasangan premis konklusi seperti yang telah kita kemukakan tersebut. Susunan kemungkinan yang dapat terjadi adalah sebagai berikut.
Dalam penyimpulan tidak langsung terdapat dua bentuk utama penalaran tidak langsung yaitu induksi dan deduksi
Terdapat beberapa kesalahan yang sering terjadi yaitu pemahaman bahwa deduktif adalah dari umum ke khusus dan induktif dari khusus ke umum. Hal yang seperti ini tidak tepat karena deduktif belum tentu dari umum ke khusus, dapat juga dari umum ke umum. Perbedaan pokok antara keduanya adalah terletak pada sifat kesimpulannya.
Logika deduktif, sifat kesimpulannya pasti, sedang logika induktif, sifat kesimpulannya boleh jadi atau bersifat kemungkinan.
Logika deduktif adalah sistem penalaran yang menelaah prinsip-prinsip penyimpulan yang sah berdasarkan bentuknya serta kesimpulan yang dihasilkan sebagai kemestian diturunkan dari pangkal-pikirnya. Dalam logika ini yang terutama ditelaah adalah bentuk dari kerjanya akal jika telah runtut dan sesuai dengan pertimbangan akal yang dapat dibuktikan tidak ada kesimpulan lain maka proses penyimpulannya adalah tepat dan sah. Misal:
Contoh di atas berpangkal dari pernyataan yang sudah dianggap benar sebagai titik tolak penalaran, yaitu “logam dipanaskan memuai”. Kemudian pernyataan kedua merupakan sesuatu bagian dari logam yaitu emas sehingga dirumuskan “emas adalah logam”. Pernyataan ketiga merupakan kesimpulan yang dapat ditarik dari hubungan dua pernyataan tersebut, yaitu “emas dipanaskan memuai”.
Bentuk dalam pernyataan yang dimaksudkan adalah bentuk logika, yaitu struktur dari suatu pernyataan meskipun berbeda materinya dapat juga struktur logikanya sama, misal beberapa pernyataan berikut:
Keempat pernyataan di atas materinya tidak akan sama, akan tetapi struktur logikanya adalah sama, yaitu:
“Bangsa Indonesia berketuhanan Yang Maha Esa”, diabstraksikan menjadi “semua A adalah B”. “Semua manusia berakal budi”, diabstraksikan juga sama “semua A adalah B”. “Setiap warga negara sama kedudukannya dalam pemerintahan”, diabstraksikan juga sama “semua A adalah B”. “Indonesia adalah negara berdasar atas hukum”, diabstraksikan juga sama yaitu “semua A adalah B”.
Berdasarkan struktur logika sebagaimana diuraikan tersebut maka contoh penalaran deduktif di atas dapat dirumuskan sebagai berikut.
Logika deduktif, karena berbicara tentang hubungan bentuk-bentuk pernyataan saja yang utama terlepas isi apa yang diuraikan maka logika deduktif sering disebut pula logika formal. Sering juga hanya disebut dengan logika. Jadi, jika hanya disebut logika berarti logika deduktif atau logika formal.
Cara berpikir deduksi terbagi atas silogisme kategorik, silogisme hipotetik, silogisme alternatif, dan entimem. Silogisme adalah suatu proses penalaran yang berusaha menghubungkan dua proposisi yang berlainan untuk menurunkan suatu kesimpulan yang merupakan proposisi ketiga.
Sebelum menyusun silogisme kita terlebih dahulu mengetahui hukum-hukum dalam silogisme. Dengan menggunakan hukum silogisme susunannya tepat atau tidak, sahih atau tidak sahih dapat kita ketahui. Hukum silogisme itu sebagian mengenai unsur term dan sebagian lagi mengenai unsur proposisi dalam silogisme.
Berikut hukum-hukum silogisme :
Hukum silogisme mengenai term.
Silogisme memunyai tiga term, yakni term subjek (S), term predikat (P), dan term antara (M). Hukum silogisme yang pertama sebagai berikut.
Jumlah term dalam silogisme tidak boleh lebih dari tiga. S-M-P. Hukum ini rumusan operasional dari prinsip persamaan. Dalam silogisme term tengah adalah pembanding yang digunakan untuk mengetahui apakah subjek S sama dengan predikat P atau tidak. Hasil dari pembandingan itu adalah S = P atau S ≠ P. Inilah konklusi silogisme.
Term tengah (M) tidak boleh terdapat dalam konklusi. Hukum silogisme ini dapat pula dijelaskan dengan cara memperhatikan fungsi term tengah. Term tengah pada dasarnya berfungsi mengadakan perbandingan dengan term-term lainnya dalam kedua premis. Oleh karena itu term tengah hanya diperlukan dalam premis-premis saja, dan bukan dalam konklusi.
Term tengah (M) setidak-tidaknya satu kali harus berdistribusi. Silogisme itu suatu bentuk penalaran dan seperti semua penalaran, menyimpulkan suatu konklusi dari premisnya, yang berarti bahwa premis itu sudah terkandung dalam premisnya. Tidak mungkin konklusi mengadakan sesuatu yang secara implisit belum terdapat di dalam premis. Kesatuan berpikir seperti ini akan terjadi apabila term S atau P di dalam konklusi lebih luas daripada term S atau P dalam premis.
Term S dan P dalam konklusi tidak boleh lebih luas daripada dalam premis. Kesesatan yang melanggar hukum ini banyak terjadi dan dinamakan dalam bahasa latin dengan latius hos.
Hukum silogisme mengenai proposisi.
Hukum pertama mengenai proposisi dalam silogisme adalah rumus opersional dari prinsip persamaan. Prinsip ini terdiri dari tiga anggota, berupa tiga proposisi, dua proposisi afirmatif sebagai premis yaitu S = M dan M = P, dan yang ketiga sebagai konklusinya, yaitu S = P, yang juga sebuah proposisi afirmatif. Hukum silogisme itu adalah.
Apabila proposisi-proposisi dalam premis afirmatif, maka konklusinya harus afirmatif. Menurut prinsip perbedaan, tidak mungkin proposisi-proposisi dalam premis itu semuanya negatif, salah satu pasti harus afirmatif; S = M dan M ≠ P atau sebaliknya. Kalau kedua proposisi dalam premis itu negatif, tidak ada term yang berfungsi sebagai term tengah, tidak ada term yang menghubungkan term S dan term P. Kalau S ≠ M dan M ≠ P maka term M tidak berfungsi term tengah, artinya tidak menghubungkan term S dengan P.
Proposisi di dalam premis tidak boleh kedua-keduanya negatif. Menurut prinsip perbedaan pula, kecuali proposisi dalam premis itu harus yang satu afirmatif dan yang lainnya negatif, maka konklusinya pasti negatif. Proposisi afirmatif itu dipandang proposisi kuat, sedangkan proposisi negatif itu proposisi lemah.
Konklusi mengikuti proposisi yang lemah dalam premis. Hukum ini harus diartikan bahwa kalau di dalam premis ada proposisi partikular, maka konklusinya pun harus partikular. Sebab penilaian kuat atau lemah itu juga mengenai kuantitas proposisi. Dalam hal ini, proposisi universal adalah proposisi kuat, sedangkan proposisi partikular adalah lemah. Bahwa konklusinya harus mengikuti proposisi partikular yang terdapat di dalam premis adalah jelas. Jika tidak demikian akan terjadi kesesatan Latius Hos, term S di dalam konklusi akan lebih luas daripada di dalam premis.
Proposisi dalam premis tidak boleh kedua-duanya partikular, setidak-tidaknya salah satu harus universal. Hukum ini sebenarnya hanya merupakan pelaksanaan hukum ketiga atau keempat di atas mengenai term. Pelanggaran terhadap hukum tiga atau empat, tergantung bentuk silogismenya. Dua proposisi yang partikular dalam premis itu kedua-duanya proposisi afirmatif atau salah satu diantaranya adalah proposisi negatif.
Silogisme Kategorik
Silogisme adalah suatu bentuk formal deduksi yang terdiri dari proposisi- proposisi kategori. Konklusi dalam silogisme ditarik dari proposisi I dengan bantuan proposisi II. Tanpa adanya proposisi II tidak dapat ditarik sebuah konklusi. Jadi, kedua proposisi itu merupakan dasar bagi penarikan sebuah konklusi.
Silogisme kategorik merupakan struktur suatu deduksi berupa suatu proses logis yang terdiri dari tiga bagian yang masing-masing bagiannya berupa pernyataan kategoris atau pernyataan tanpa syarat.
Contoh 1
Proposisi I : Semua sarjana adalah tamatan S1.
Proposisi II : Daniel adalah sarjana.
Konklusi : Daniel tamatan S1.
Contoh 2
Proposisi I : Semua tanaman membutuhkan air.
Proposisi II : Akasia adalah tanaman.
Konklusi : Akasia membutuhkan air.
Silogisme Hipotetik
Silogisme hipotetis atau silogisme pengandaian adalah semacam pola penalaran deduktif yang mengandung hipotesis. Silogisme ini bertolak dari suatu pendirian, bahwa ada kemungkinan apa yang disebut dalam proposisi itu tidak ada atau tidak terjadi. Premis mayornya mengandung pernyataan yang bersifat hipotesis, dan premis minornya mengandung pernyataan apakah kondisi pertama terjadi atau tidak. Rumus proposisi mayor dari silogisme ini adalah jika P maka Q.
Jenis-jenis silogisme hipotetik sebagai berikut.
Silogisme hipotetik yang premis minornya mengakui bagian anteseden, seperti:
Premis Mayor : Jika hujan, saya naik becak.
Premis Minor : Sekarang hujan.
Kesimpulan : Jadi, saya naik becak.
Silogisme hipotetik yang premis minornya mengakui bagian konsekuennya, seperti:
Premis Mayor : Bila hujan, bumi akan basah.
Premis Minor : Sekarang bumi telah basah.
Kesimpulan : Jadi, hujan telah turun.
Silogisme hipotetik yang premis minornya mengingkari anteseden, seperti:
Premis Mayor :Jika politik pemerintah dilaksanakan dengan paksa, maka kegelisahan akan timbul.
Premis Minor : Politik pemerintahan tidak dilaksanakan dengan paksa,
Kesimpulan : Jadi, kegelisahan tidak akan timbul.
Silogisme hipotetik yang premis minornya mengingkari bagian konsekuennya, seperti:
Premis Mayor : Bila mahasiswa turun ke jalanan, pihak penguasa akan gelisah.
Premis Minor : Pihak penguasa tidak gelisah.
Kesimpulan : Jadi, mahasiswa tidak turun ke jalanan.
Bila anteseden kita lambangkan dengan A dan konsekuen dengan B maka, hukum silogisme hipotetik adalah sebagai berikut.
Bila A terlaksana maka B juga terlaksana.
Bila A tidak terlaksana maka B tidak terlaksana. (tidak sah = salah)
Bila B terlaksana, maka A terlaksana. (tidak sah = salah)
Bila B tidak terlaksana maka A tidak terlaksana.
Silogisme Alternatif
Silogisme alternatif merupakan silogisme yang proposisi mayornya mengandung kemungkinan atau pilihan. Proposisi minornya menerima atau menolak salah satu alternatif itu. Konklusinya bergantung pada premis minor. Jika premis minor menolak satu alternatif, maka alternatif lain diterima.
Silogisme alternatif adalah silogisme yang premis mayornya keputusan alternatif sedangkan premis minornya kategorik yang mengakui atau mengingkari salah satu alternatif yang disebut oleh premis mayor. Rumus Silogisme Alternatif
Premis Mayor : A atau B
Premis Minor : Bukan A atau bukan B
Kesimpulan : Jadi B (atau) A
Contoh 1
Premis Mayor : Andi mencintai saya atau membenci saya.
Premis Minor : Andi tidak mencintai saya
Kesimpulan : Maka, Andi membenci saya.
Contoh 2
Premis Mayor : Hasan di rumah atau di pasar.
Premis Minor : Hasan tidak di rumah.
Kesimpulan : Jadi, Hasan di pasar
Hukum-hukum silogisme alternatif dapat dijelaskan sebagai berikut.
Bila premis minor mengakui salah satu alternatif, maka konklusinya sah (benar).
Contoh: Budi menjadi guru atau pelaut. Budi adalah guru. Maka Budi bukan pelaut.
Bila premis minor mengingkari salah satu alternatif, maka konklusinya tidak sah (salah).
Contoh: Penjahat itu lari ke Solo atau ke Yogya. Ternyata tidak lari ke Yogya. Maka dia lari ke Solo.
Konklusi ini salah karena bisa jadi dia lari ke kota lain.
Bentuk penalaran kedua selain logika deduktif adalah logika induktif. Logika induktif adalah sistem penalaran yang menelaah prinsip-prinsip penyimpulan yang sah dari sejumlah hal khusus sampai pada suatu kesimpulan umum yang bersifat boleh jadi. Logika ini sering disebut juga logika material, yaitu berusaha menemukan prinsip-prinsip penalaran yang bergantung kesesuaiannya dengan kenyataan, oleh karena itu kesimpulannya hanyalah kebolehjadian, dalam arti selama kesimpulannya itu tidak ada bukti yang menyangkalnya maka kesimpulan itu benar, dan tidak dapat dikatakan pasti. Misal:
Contoh tersebut berpangkal pada sejumlah hal khusus, yaitu dari tiga materi yang berupa logam, besi, dan perak. Oleh karena berpangkal pada materi maka tepat jika disebut dengan logika material dan kesimpulannya bersifat kemungkinan atau kebolehjadian, boleh jadi benar boleh jadi tidak benar.
Logika induktif merupakan pokok bahasan metodologi ilmiah, atau dengan kata lain metodologi ilmiah merupakan perluasan dari logika induktif sehingga logika induktif disebut juga “Metode-metode Ilmiah”.
Proses penalaran induktif banyak sekali jenisnya, yaitu dapat berupa generalisasi, analogi induktif, dan hubungan sebab-akibat.
Generalisasi
Generalisasi adalah suatu proses penalaran yang bertolak dari sejumlah fenomena individual untuk menurunkan suatu kesimpulan yang bersifat umum yang mencakup semua fenomena itu atau menuju kesimpulan umum yang mengikat seluruh fenomena sejenis dengan fenomena individual yang diselidiki.
Dalam logika induktif tidak ada konklusi yang memunyai nilai kebenaran yang pasti. Namun, hanyalah probabilitas rendah atau tinggi. Dalam generalisasi induktif adalah semakin besar jumlah fakta yang dijadikan dasar penalaran induktif, maka semakin tinggi probabilitas konklusinya, dan sebaliknya semakin sedikit jumlah fakta yang dijadikan dasar penalaran induktif, maka semakin rendah probabilitas konklusinya.
Contoh:
Raisa adalah bintang iklan, dan ia berparas cantik.
Sandra Dewi adalah bintang iklan, dan ia berparas cantik.
Raisa dan Sandra Dewi adalah bintang iklan. Jadi, semua bintang iklan berparas cantik.
Analogi
Pikiran itu berangkat dari suatu kejadian khusus ke sesuatu kejadian khusus lainnya yang semacam dan menyimpulkan bahwa yang benar pada yang satu juga akan benar pada yang lain. Dengan kata lain analogi adalah suatu proses penalaran yang bertolak dari dua peristiwa khusus yang mirip satu sama lain, kemudian menyimpulkan bahwa apa yang berlaku untuk suatu hal akan berlaku pula untuk hal yang lain.
Analogi pada dasarnya membandingkan dua hal, dan mengambil kesamaan dari dua hal tersebut.
Contoh:
Sheila berwajah putih karena memakai bedak padat.
Keysia juga ikut memakai bedak padat agar berwajah putih.
Dari contoh di atas Keysia menggunakan penalaran analogi induktif. Karena, ia menarik simpulan jika memakai bedak padat maka wajahnya akan putih seperti Sheila.
Hubungan Sebab Akibat
Penalaran jenis ini dimulai dari suatu peristiwa sehingga sampai pada suatu kesimpulan bahwa peristiwa itu adalah suatu keadaan atau peristiwa tersebut akibat suatu keadaaan.
Contoh:
Kemarau tahun ini cukup panjang. Sebelumnya, pohon-pohon di hutan yang berfungsi sebagai penyerap air banyak yang ditebang. Selain itu, irigasi di desa Sidomulyo tidak lancar. Ditambah lagi dengan harga pupuk yang semakin mahal serta kurangnya pengetahuan para petani dalam menggarap lahan tanahnya. Oleh karena itu, tidak mengherankan jika panen di desa ini selalu gagal.
Hubungan Akibat Sebab
Hubungan sebab akibat merupakan pemikiran yang berawal dari suatu akibat yang diketahui ke sebab yang mungkin menghasilkan akibat tersebut. Hubungan akibat sebab ini merupakan pembalikan dari hubungan sebab akibat.
Contoh:
Ayah akan pergi ke rumah pak Tono. Ia pergi dengan mengendarai motor. Di tengah perjalanan motor yang dikendarai Ayah mogok. Lalu Ayah mencari penyebab motornya mogok, dan ternyata bensin motor Ayah habis.
Secara etimologis, logika adalah istilah yang dibentuk dari kata logikos yang berasal dari kata benda logos yang berarti sesuatu yang diutarakan, suatu pertimbangan akal (pikiran), kata, percakapan, atau ungkapan lewat bahasa.
Logika adalah salah satu cabang filsafat. Sebagai ilmu, logika disebut dengan logike episteme (Latin: logica scientia) atau ilmu logika (ilmu pengetahuan) yang mempelajari kecakapan untuk berpikir secara lurus, tepat, dan teratur, namun sekarang ini lazim disebut logika saja (Rapar, Jon Hendrik.1978).
Dalam buku Pengantar Logika Modern, Gie et al. (1978) mengemukakan dewasa ini logika telah mulai mendapat pengakuan dalam bidang pendidikan di Indonesia dengan kehadiran berbagai buku logika dalam bahasa Indonesia, namun memberikan gambaran yang kurang tepat mengenai logika.
Beberapa batasan dan pengertian logika antara lain :
Dalam buku Pembimbing Ke Filsafat dan Logika Formal (tanpa tahun) Prof. Dr. N. Drijarkara telah membatasi pengertian logika yaitu, “Logika adalah ilmu pengetahuan yang memandang hukum-hukum susunan atau bentuk pikiran manusia, juga menyebabkan pikiran dapat mencapai kebenaran.”
Batasan logika dalam buku Epistemologi : Bentuk Seni Teori Berfikir Ilmiah Bahagian Logika, Jilid II, cetakan II (1974/stensil) karangan Drs. R.B.S. Fudyartanta, “Logika adalah salah satu cabang filsafat. Oleh karena itu logika sebagai filsafat berarti ilmu yang sedalam-dalamnya tentang kebenaran berpikir.
Artinya mencari kebenaran yang tertinggi, yang hakiki daripada berpikir. Pendek kata logika adalah ilmu yang radikal tentang berpikir yang benar, supaya hasilnya benar. Dengan mempelajari dan mempergunakan logika sebagai ilmu filsafat berpikir, maka akan ditemui berbagai metodos berpikir dengan berbagai rumusan dan bahan-bahan yang dipikirkan.”
Drs. Nuril Huda dalam Prakata buku Logika Praktis Jilid I (1974/stensil) yang merupakan saduran dari buku Applied Logic karya Little, Wilson & Moore, menguraikan definisi logika sebagai berikut, “Diperlukan hukum-hukum dan kaidah-kaidah berpikir untuk mengontrol proses berpikir yang panjang dan berlibat-libat. Hukum-hukum dan kaidah-kaidah berpikir itu terdapat dalam satu cabang ilmu yang disebut logika.
Dengan kata lain, logika adalah ilmu yang mempelajari dan merumuskan kaidah-kaidah dan hukum-hukum sebagai pegangan untuk berpikir tepat dan praktis bagi mencapai kesimpulan-kesimpulan yang valid dan pemecahan persoalan yang bijaksana.”
A.B. Hutabarat dalam bukunya yang berjudul Logika (1967) yang merupakan terjemahan bebas karya Dr. A. Vloemans “Voorbereiding tot de Wijsbegeerte” dan Regis Jolivet “Beknopt Handboek der Wijsbegeerte”, juga mendefinisikan logika sebagai berikut :
“Yang diartikan dengan logika adalah ilmu berpikir yang tepat dan dapat menunjukkan adanya kekeliruan didalam proses pemikiran sehingga kekeliruan itu dapat dielakkan. Maka logika dapat disebut teknik berpikir. Sebagai ilmu berpikir yang tepat maka tujuannya adalah untuk memperjelas isi dari suatu pengertian”
Dalam buku Logika : Filsafat Berpikir (1969), I. R. Poedjawijatna menjelaskan bahwa : “Logika adalah filsafat budi (manusia) yang mempelajari teknik berpikir untuk mengetahui bagaimana manusia berpikir dengan semestinya (seharusnya)”
Pada dasarnya logika tidak lepas dari penalaran logis (logical reasoning). Maka logika dan kelahirannya tidak bisa lepas dari filsafat atau pemikiran ilmiah pada umumnya.
Pembagian Logika
Terdapat macam-macam logika dilihat dari kriteria tertentu,
Logika kodratiah. Logika kodratiah adalah kemampuan berlogika yang sudah ada pada setiap manusia sebagai makhluk yang berakal budi. Tanpa belajar logika setiap orang sudah memiliki kemampuan berlogika kodratiah.
Logika ilmiah. Logika ilmiah adalah kemampuan berlogika yang didapatkan dengan belajar secara khusus. Contohnya seperti dengan membaca buku, maka mendapatkan kemampuan logika ilmiah. Semua pahlawan adalah orang berjasa (Premis mayor) Term medius (M) Term mayor §.
Logika klasik / tradisional. Logika yang diperkenalkan oleh Aristoteles pada sekitar abad ke-5 sebelum masehi; menggunakan lambang bahasa; disebut juga logika aristotelian atau logika tradisional.
Logika modern. Logika yang dikembangkan di zaman modern oleh tokoh-tokoh seperti A. de Morgan (1809-1871), George Boole (1815-1864), Bertrand Russel (1872-1970); menggunakan lambang non bahasa. Logika ini menerapkan prinsip-prinsip matematika pada logika modern; sering disebut juga logika matematika atau logika simbolik.
Logika formal (bentuk). Logika formal adalah logika yang membahas kebenaran sebuah argumen dilihat dari segi bentuk. Kebenaran bentuk adalah kebenaran yang dimiliki sebuah argumen.
Logika material (isi). Logika material adalah logika yang membahas kebenaran sebuah argumen dilihat dari segi isinya Sebuah argumen dinyatakan benar dari segi isi jika pernyataan yang terdapat dalam argumen sesuai dengan kenyataan.
Logika induktif. Logika induktif adalah bentuk penalaran yang berdasarkan kebenaran-kebenaran tunggal yang ditarik menjadi satu kesimpulan umum, biasa dikenal sebagai metode induktif.
Logika deduktif. Logika deduktif adalah suatu ragam logika yang mempelajari asas-asas penalaran yang bersifat deduktif, yaitu penalaran yang berdasarkan kebenaran umum (atau yang sudah ada) ditarik satu kesimpulan untuk hal yang khusus (kebenaran baru).
Logika adalah setiap mode analisis yang mengikuti mode dan dapat diterima untuk membuat kesimpulan dari data yang diberikan. Arti lainnya yakni cabang filsafat dan matematika yang berkaitan dengan bentuk-bentuk inferensi yang mengarah pada kesimpulan yang valid dari premis-premis yang diterima. Arti lainnya yakni penciptaan bahasa simbolik dengan aturan untuk deduksi dan inferensi yang ditetapkan sebagai bagian dari sistem simbol dan sering disebut logika simbolik.
Sumber : David Matsumoto, The Cambridge Dictionary of Psychology
