Kata regresi pertama kali dikenalkan oleh Francis Galton, yang menceritakan tentang keterkaitan hubungan antara tinggi badan anak dengan orang tuanya. Secara umum, analisis regresi dapat diartikan sebagai berikut,
Analisis regresi berkaitan dengan studi mengenai ketergantungan satu variabel, yaitu variabel dependen atau variabel tergantung terhadap satu atau lebih variabel lainnya, yaitu variabel independen atau variabel bebas. Analisis ini dilakukan untuk melakukan estimasi dan atau memperkirakan nila rata-rata (populasi) variabel dependen dari nilai yang diketahui pada variabel independen atau variabel bebas, dalam sampling berulang (repeated sampling).
Atau dengan kata lain, analisis regresi adalah suatu metode analisis data yang menggambarkan hubungan fungsional antara variabel dependen dengan satu atau beberapa variabel independen.
Misalkan X adalah variabel independen dan Y adalah variabel dependen untuk n data pengamatan berpasangan, maka hubungan antara variabel dependen dan variabel independen tersebut dapat dinyatakan sebagai berikut:
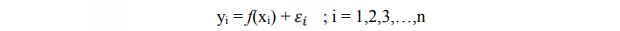
Dengan persyaratan bahwa error (ε) diasumsikan independen, datanya menyebar secara normal, dan mempunyai variansi yang konstan. f(xi) disebut sebagai fungsi regresi atau kurva regresi (Hardle,1994)
Analisis Regresi Linear Sederhana
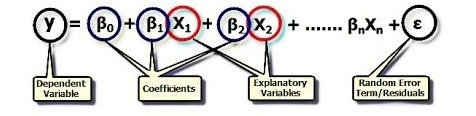
Dalam analisis regresi linear sederhana akan ditentukan persamaan yang menghubungkan dua variabel yang dapat dinyatakan sebagai bentuk persamaaan pangkat satu (persamaan linier / persamaan garis lurus). Dimana variabel terikat dijelaskan oleh satu variabel bebas. Persamaan umum garis regresi untuk regresi linear sederhana adalah:
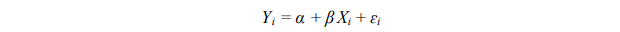
dimana,
Yi = variabel tak bebas pengamatan ke-i
Xi = variabel bebas pengamatan ke-i
α = konstanta (parameter)
β = koefisien regresi atau kemiringan / slope (parameter)
ɛi = error pengamatan ke-i
Untuk lebih jelasnya terkait dengan penggambaan persamaan analisis regresi diatas, maka dapat dijelaskan pada gambar berikut ini,
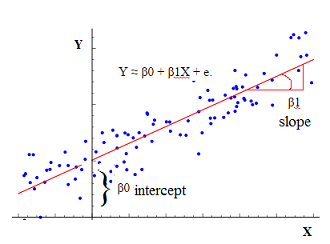
dimana
-
nilai α atau β0 merupakan sebuah titik potong sumbu Y, dalam artian, apabila nilai x = 0 maka nilai Y adalah sebesar α.
-
nilai β1 adalah kemiringan atau slope dari garis persamaan, dengan rumus β1 = dy/dx
Dalam regresi linier sederhana, yang akan diduga atau diperkirakan adalah nilai α dan β. Sehingga persamaan linier untuk perkiraan atau pendugaan garis regresi linier ditulis dalam bentuk :
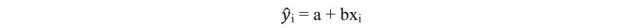
dimana,
ŷ = nilai dugaan variabel terikat pengamatan ke-i
xi = nilai variabel bebas pengamatan ke-i
a = titik potong garis regresi pada sumbu-y atau nilai dugaan bila x = 0
b = gradien garis regresi (perubahan nilai dugaan per satuan perubahan nilai x)
Asumsi Analisis Regresi Linear
Agar dapat ditarik kesimpulan yang benar tentang parameter α dan β, terdapat persyaratan-persyaratan yang harus dipenuhi. Persyaratan tersebut biasanya disebut dengan asmusi. Asumsi-asumsi model regresi yang harus terpenuhi (Drapper dan Smith, 1992) adalah :
-
Nilai ɛi adalah bebas satu dengan yang lainnya atau korelasi (ɛi , ɛj) = 0. Untuk asumsi pertama yang menyatakan independen, artinya ɛi merupakan variabel acak dengan nilai tengah nol dan ragam σ2 yang tidak diketahui.
-
E(ɛi) = 0, V(ɛj) = σ2. ɛi dan ɛj tidak berkorelasi, i ≠ j , sehingga covv(ɛi ɛi) = 0, atau dalam artian tidak ada korelasi antara ɛi ɛi.
-
E(Yi ) = α + βXi , Yi dan Yj , i ≠ j , atau dalam artian tidak ada korelasi antara ɛi dengan variabel dependen (x). ɛi merupakan variabel acak normal, dengan nilai tengah nol dan ragam σ2 ɛ dengan kata lain ɛi ~ N (0, σ2ɛ).
-
Nilai tengah dari Y adalah fungsi linier dari X, yaitu jika dihubungkan titik-titik dari nilai tengah yang berbeda, maka akan diperoleh garis lurus µ(y/x) = α + β X.
Untuk asumsi kedua yang disebut garis linier, artinya X mempunyai hubungan linier dengan Y. Nilai tengah Y untuk kombinasi tertentu dari nilai X adalah fungsi linier dari X, yaitu µY|X .
ɛ adalah variabel acak dengan µ = 0 untuk nilai X yang tetap, sehingga µɛ|X = 0 untuk sembarang X, dengan nilai X yang tetap maka nilai E(Y) = E(βX) = βX.
ɛ menggambarkan seberapa jauh setiap Y menyimpang dari regresi populasinya. Yang dimaksud dengan kelinieran adalah linier dengan koefisien. Jika hubungan titik-titik dari nilai tengah µY|X yang berbeda akan diperoleh garis lurus.
Asumsi ini diperlukan agar uji-uji statistik seperti uji F dan uji t menjadi signifikan.
-
Ragam galat homogen (homoskedastik) yaitu galat memiliki nilai ragam yang sama antara galat ke-i dan galat ke-j. Secara matematis ditulis Var (ɛi) = σ2 ; i = 1,2,. . . , n dan n = banyaknya pengamatan.
Untuk asumsi ketiga yang menyatakan varian Y adalah sama untuk setiap kombinasi tetap X; yaitu σ2 Y|X = var (Y|X) = σ2 untuk semua X.
Asumsi ini sering dikenal dengan sebutan homoscedasticity, dengan homo berarti sama scedastic berarti sebaran. Model regresi menganggap galat menyebar secara normal disekitar nilai tengah nol, dan mempunyai ragam yang sama. Banyak metode yang dapat dipergunakan untuk memeriksa apakah asumsi ini terpenuhi atau tidak, salah satunya adalah dengan metode Glejser.
Kehomogenan diperlukan agar uji-uji statistik seperti uji F dan uji t menjadi signifikan.
-
Ragam galat menyebar normal dengan rata-rata nol dan suatu ragam tertentu. Asumsi keempat menyatakan untuk sembarang kombinasi tetap dari variabel bebas X, variabel tak bebas Y berdistribusi normal atau yang biasa disebut asumsi kenormalan. Dengan kata lain Y ~ N (µY|X, σ2). E(Y) = E(Xβ) + E(ɛ) dengan E(ɛ) = 0 sehingga E(Y) = (Xβ) dan Var (Y) = Var (X + β ) = Var (ɛ) = σ2.
ɛi merupakan variabel acak dengan nilai tengah nol dan ragam σ2, sehingga ɛ ~ N (0, σ2).
Sebaran normal diperlukan agar uji t maupun uji F dapat dilakukan. Kenormalan bisa dilihat secara eksploratif melalui plot sisaan sedangkan untuk uji formalnya dapat digunakan uji Kolmogorov-Smirnov.
Pengujian asumsi-asumsi tersebut diatas, biasanya dilakukan dengan melakukan uji asumsi klasik.