Apa yang dimaksud dengan Analisis Regresi Berganda?

Matematika Statistika
1

Analisis Regresi Berganda

Analisis regresi berganda adalah suatu metode untuk meramalkan nilai pengaruh dua variabel independen atau lebih terhadap satu variabel dependen.

Apa yang dimaksud dengan Analisis Regresi Berganda ?

2

Analisis regresi merupakan analisis statistika yang digunakan untuk mengetahui hubungan antara variabel dependen dengan variabel independen. Apabila hanya terdapat satu variabel dependen dan satu variabel independen disebut analisis regresi sederhana, sedangkan apabila terdapat beberapa variabel independen disebut analisis regresi ganda. Secara umum, model regresi linear ganda dengan variabel dependen Y dan p variabel bebas 𝑋1,𝑋2, … , 𝑋𝑝 dapat ditulis sebagai berikut:

image

dimana:
𝑌1𝑖 : nilai variabel dependen dalam pengamatan ke-i
𝛽0, 𝛽1, 𝛽2, … , 𝛽𝑝 : parameter yang tidak diketahui nilainya
𝑋𝑖1, 𝑋𝑖2, … , 𝑋𝑖𝑝 : nilai dari variabel independen dari pengamatan ke-i
𝜀𝑖 : galat yang bersifat acak dan berdistribusi normal N (0, 𝜎2)

Selain menggunakan notasi di atas, penggunaan matriks terhadap regresi linear mempunyai banyak keuntungan yaitu menyajikan bentuk yang ringkas untuk menangani model regresi yang memuat banyak variabel . Persamaan di atas merupakan penjabaran dari himpunan n persamaan simultan :

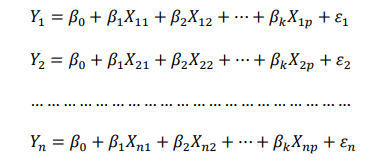
image

Dalam lambang matriks menjadi

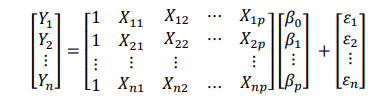
image

Persamaan di atas juga dapat ditulis secara sederhana

image

dimana :
Y : vektor pengamatan variabel dependen yang berukuran 𝑛𝑥1
X : variabel independen yang berukuran 𝑛𝑥(𝑝 + 1)
𝜷 : vektor koefisien variabel independen yang berukuran (𝑝 + 1)𝑥1
𝜺 : vektor galat yang berukuran 𝑛𝑥1
𝑖 : 1,2,…n menunjukkan banyaknya pengamatan

Asumsi Regresi Linier

Asumsi-asumsi regresi linear klasik adalah sebagai berikut:

  1. Nilai harapan dari galat adalah nol, 𝐸(𝜀𝑖) = 0 dan variansi galat sama yaitu merupakan nilai konstan sebesar 𝜎2
  2. Galat berdistribusi normal dengan rata-rata nol dan variansi 𝜎2, 𝜀𝑖~𝑁(0, 𝜎2)
  3. Tidak terjadi korelasi antar galat sehingga kovariannya adalah nol, 𝑐𝑜𝑣(𝜀𝑖, 𝜀𝑗) = 0, 𝑖≠𝑗
  4. Tidak terjadi korelasi antara variabel bebas X atau tidak terdapat multikolinearitas antara variabel bebas X