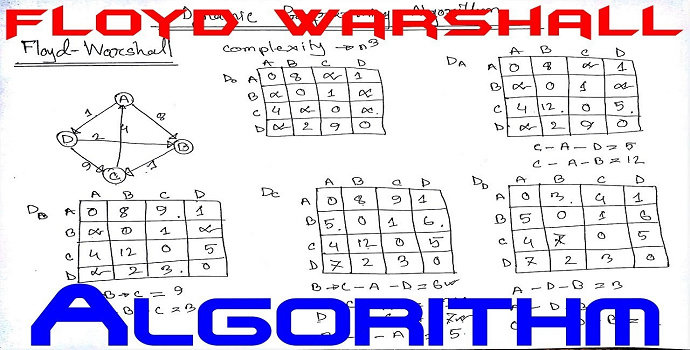
Algoritma Floyd-Warshall merupakan algoritma yang digunakan untuk mencari lintasan terpendek pada sebuah graf berbobot dengan bobot positif atau negatif (namun tidak memiliki siklus negatif).
Apa yang anda ketahui tentang Algoritma Floyd-Warshall ?
Algoritma Floyd-Warshall adalah sebuah algoritma analisis graf untuk mencari bobot minimum dari graf berarah. Algoritma Floyd-Warshall adalah matriks hubung graf berarah berlabel, dan keluarannya adalah path terpendek dari semua titik ke titik yang lain (Kamayudi,2009).
Dalam usaha untuk mencari path terpendek, Algoritma Warshall memulai iterasi dari titik awalnya kemudian memperpanjang path dengan mengevaluasi titik demi titik hingga mencapai titik tujuan dengan jumlah bobot yang seminimum mungkin. Misalkan
𝑊𝑊0 adalah matriks hubung graf berarah berlebel mula-mula. 𝑊𝑊∗ adalah matriks hubung minimal dengan 𝑊𝑊𝑖𝑖𝑗𝑗 ∗ = path terpendek dari titik 𝑣𝑣𝑖𝑖 ke 𝑣𝑣𝑗𝑗 .[4]
Algoritma Warshall untuk mencari path terpendek adalah sebagai berikut
Dalam iterasinya untuk mencari path terpendek, Algoritma Warshall membentuk n matriks sesuai dengan iterasi-k. Hal ini menyebabkan waktu prosesnya lambat, terutama untuk n yang besar. Meskipun waktu prosesnya bukanlah yang tercepat, Algoritma Warshall sering dipergunakan untuk menghitung path terpendek karena kesederhanaannya.
Program implementasinya Algoritma Warshall sangat mudah dibuat.
function fw(int[1..n,1..n] graph) {
// Inisialisasi
var int[1..n,1..n] jarak := graph
var int[1..n,1..n] sebelum
for i from 1 to n
for j from 1 to n
if jarak[i,j] < Tak-hingga
sebelum[i,j] := i
// Perulangan utama pada algoritme
for k from 1 to n
for i from 1 to n
for j from 1 to n
if jarak[i,j] > jarak[i,k] + jarak[k,j]
jarak[i,j] = jarak[i,k] + jarak[k,j]
sebelum[i,j] = sebelum[k,j]
return jarak
}